Задача по теории Галуа

[nnosipov]

Да, нужно всё-таки привести пример многочлена с дискриминантом, который точный квадрат.

$a$ --- это корень из дискриминанта.

[DoubleBubble]

$x^3-3x+1$
если я всё верно понял, то $D = -4p^3 - 27q^2 = 4\cdot 27 - 27 = 3\cdot 27 = 9^2$

[nnosipov]

Да, это хороший пример. Здесь даже можно корни выписать в виде простых выражений. Рекомендую попробовать (хотя для решения исходной задачи это необязательно).

[DoubleBubble]

Но ещё остались несколько вопросов.
Почему если два корня выражаются через первый, то степень расширения будет 3?

[nnosipov]

DoubleBubble в сообщении #797275 писал(а):

Почему если два корня выражаются через первый, то степень расширения будет 3?

Не просто выражаются, а рационально выражаются. Вот с этим вопросом попробуйте сами разобраться, это простой вопрос.

[DoubleBubble]

Я понимаю, что для этого нужно просто воспользоваться определением, но я не смог его найти. Ну, кроме как что это будет $dim_\mathbb{Q}\mathbb{Q}(x_1,x_2,x_3)$

[nnosipov]

DoubleBubble в сообщении #797277 писал(а):

Я понимаю, что для этого нужно просто воспользоваться определением, но я не смог его найти. Ну, кроме как что это будет $dim_\mathbb{Q}\mathbb{Q}(x_1,x_2,x_3)$

Да. Осталось понять, что $\mathbb{Q}(x_1,x_2,x_3)=\ldots$ чему?

[DoubleBubble]

$\mathbb{Q}(x_1,x_2,x_3)=\mathbb{Q}(x_1)$.
Но ведь $\mathbb{Q}$ над $\mathbb{Q} $ является пространством размерности 1.
Мы добавляем иррациональный элемент $x_1$ и $\mathbb{Q}(x_1)$ имеет размерность 2, потому что $x_1 \notin \mathbb{Q}$?

[nnosipov]

DoubleBubble в сообщении #797279 писал(а):

Мы добавляем иррациональный элемент $x_1$ и $\mathbb{Q}(x_1)$ имеет размерность 2, потому что $x_1 \notin \mathbb{Q}$?

Почему 2? Ведь $x_1$ --- корень кубического многочлена, причём неприводимого над $\mathbb{Q}$. Значит, не 2, а ... сколько?

[DoubleBubble]

Окей, видимо, раз многочлен неприводим и степени 3, то $x_1,x_1^2\notin\mathbb{Q}$ и тогда степень расширения будет как раз 3. Но почему так? Это можно увидеть по формуле Кардано, конечно, но хотелось бы понять.
А если бы все 3 корня были независимы, то степень расширения была бы 7?

[nnosipov]

DoubleBubble в сообщении #797284 писал(а):

Окей, видимо, раз многочлен неприводим и степени 3, то $x_1,x_1^2\notin\mathbb{Q}$ и тогда степень расширения будет как раз 3. Но почему так?
А если бы все 3 корня были независимы, то степень расширения была бы 7?

Так, Вам нужно ещё раз понять, как устроено простое алгебраическое расширение (это когда к некоторому полю присоединяют корень неприводимого многочлена степени $n$). Про это лучше прочитать в учебнике или в лекциях.

[DoubleBubble]

Что значит "как устроено"? Не могу сказать, что моё понимание особо глубокое, но то, что было дано на лекции я понимаю.
Было поле $\mathbb{Q}$, и есть элемент $x_1$, который является алгебраическим над $\mathbb{Q}$. Мы добавляем его в это поле и получаем $\mathbb{Q}(x_1)$ - алгебраическое расширение поля $\mathbb{Q}$. Также мы добавляем туда и корни $x_2,x_3$, но так как они рационально выражаются через $x_1$ - это ничего не меняет и мы по-прежнему имеем $\mathbb{Q}(x_1)$.
Это мне ясно. А вот дальше я не уверен.
Есть ещё элемент $x_1^2$, который не лежит в $\mathbb{Q}$ и не выражается рационально через $x_1$.

[ex-math]

Прошу прощения, что встреваю.
Добавив $x_1$, Вы добавляете также все его степени -- ведь у нас поле, значит, можно умножать все на все. Но вдруг оказывается, что линейно независимых над $\mathbb{Q}$ среди этих степеней всего... сколько? И каждый элемент $\mathbb{Q}(x_1)$ представляется в виде соответствующей линейной их комбинации с рациональными коэффициентами, т.е. имеем векторное пространство некоторой размерности, которую Вам и надо найти. 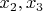А если Вы присоедините $x_2,x_3$ (в случае, когда они не выражаются рационально через $x_1$), то Вы присоедините помимо их степеней также всевозможные произведения. И они тоже не все линейно независимы над $\mathbb{Q}$ -- формулы Виета в помощь.

[DoubleBubble]

Точно. Все элементы поля $\mathbb{Q}(x_1)$ имеют вид $q = \alpha +\beta x_1+\gamma x_1^2$, где коэффициенты - рациональные числа, так?

[nnosipov]

DoubleBubble в сообщении #797299 писал(а):

Все элементы поля $\mathbb{Q}(x_1)$ имеют вид $q = \alpha +\beta x_1+\gamma x_1^2$, где коэффициенты - рациональные числа, так?

Да, вот теперь верно. Таким образом, базис $\mathbb{Q}(x_1)$ над $\mathbb{Q}$ составляют $1$, $x_1$, $x_1^2$ и, следовательно, размерность (степень расширения) равна 3. Окей?