Постройка кубированной сферы

[hardor]

Здравствуйте, возникла задача пострйки кубированной сферы.
Пусть у нас дан куб с сеткой на поверхности. В него впишем сферу, и отобразим каждый узел сферы на куб. В итоге мы получим кубированную сферу. Я нашел некоторое подобие решения задачи http://mathproofs.blogspot.ru/2005/07/m ... phere.html , но мне там непонятны формулы, 4я степень под корнем...


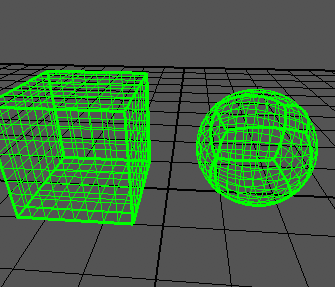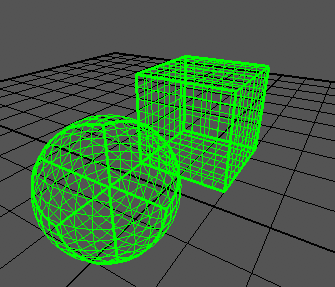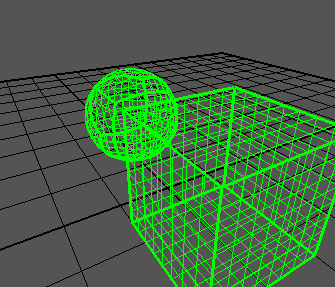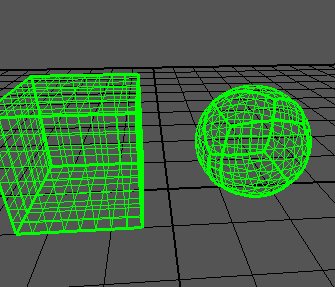
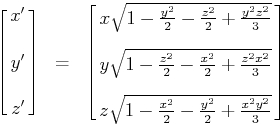
Хотелось бы найти решение через тангенсы, как я понимаю для каждой грани решения будут немного отличаться. Спасибо.

[ИСН]

Это порочный подход - отбрасывать решение потому, что оно непонятно. Обычно любое другое бывает либо такое же, либо неправильное. Здесь, правда, не так, но всё равно. Тангенсы кого Вы хотите, и зачем?

[hardor]

Через тангенсы углов между проекциями лучей на систему координат. Так как мы проецируем узлы решетки на сферу, то логично составить уравнения типа
x/y=x'/y'=tan(phi)
x/z=x'/z'=tan(psi)
x'^2+y'^2+z'^2=r^2

Трудности состовляют с разрешением такой системы. так же не надо забывать что система для каждой четверти разная

[ИСН]

А, ну это можно сделать.
1. Зачеркнуть самую правую часть первых двух уравнений (ту, что с тангенсами), потому что она пока(*) не нужна.
2. Из первого уравнения выразить y' через x' и известные величины.
3. Из второго уравнения выразить z' тоже через x' и известные величины.
4. То, что получилось, подставить в третье уравнение.

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Причина переноса: формулы не оформлены $\TeX$ом

hardor
Наберите все формулы и термы $\TeX$ом. Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.