Добрый вечер! Вопрос о бесконечности всегда интересует математиков. Сначала рассмотрим метод Кантора с логической "наивной" точки зрения. Как известно, Кантор установил существование т.н. континуума. Для этого, например, можно рассмотреть множество действительных чисел (0,1). Предположим, что эти действительные числа записываются бесконечной десятичной (сразу скажем - счетной) дробью

Предположим, что между всем этим множеством дробей и счетным множеством натуральных чисел установлено взаимно-однозначное соответствие (можно записать дроби в столбик). Теперь мы можем очевидным способом получить новое число ( у которого
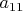
отличается и т.д.), которое не равно ни одному из рассматриваемых дробей. Вывод: множество дробей из (0, 1) "больше" множества натуральных чисел. Т. е. существует континуум. Вопрос заключается вот в чем. Мы установили существование множества континуума. Естественно предположить, что мощность дробей (0, 1) имеет мощность континуум. Докажем это. Раз континуум бесконечное множество, то имеется хотя бы один элемент. Поставим ему в соответствие дробь из (0, 1). И т.д. Теперь опять применим диагональный метод Кантора. Очевидным образом получим число, которое не будет равно ни одной дроби из (0, 1). Здесь возможно возражение. Метод называется диагональным, т.к. у него плечи должны быть равны. В бесконечной десятичной записи дробей фигурирует счетное множество цифр, а только что было доказано, что самих дробей гораздо больше и т.д. У вас цифры в десятичной записи "быстро" закончатся, а самих дробей будет еще бесконечно много. Другими словами, диагональный метод Кантора в этом случае неприменим. А мощность множества чисел (0, 1) можно просто постулировать. Что же касается диагонального метода, то, очевидно, прежде чем применить диагональный метод нужно доказать, что он здесь применим. Почему же мы не доказывали его применимость в первом рассматриваемом случае? Вот вопрос.