Множество

содержит все натуральные числа от 1 до 2013 включительно, причём если
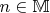
, то

содержит все члены арифметической прогрессии с первым членом

и разностью

.
Обязательно ли существует число

такое, что

содержит все натуральные числа, большие

?
Так, я не поняла, это что у нас, юмор такой, что ли?
Для любого достаточно большого простого числа

число

может не принадлежать

, а значит, число

не обязано существовать.
Неужели не так?