Вычислить интервальную оценку дисперсии нормального распределения, с надежностью 0.98 , если по выборке объема

найдена выборочная дисперсия

.
Решение я начал с поиска в учебнике, вот что нашел:
Интервальной оценкой с надежностью

среднего квадратического отклонения

нормально распределенного количественного признака

по "исправленному" выборочному среднему квадратическому отклонения

служит доверительный интервал

( при

) и

(при
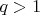
, где

находят по таблице по заданным

и

Естественно, я нашел табличку, из нее:

(приблизительно,т.к. для n=17 там дается только для надежностей 0,95 , 0,99 и 0,999 значения 0,42 0,66 и 1,01 соответственно). У нас случай с

след-но интервал такой:

Отсюда

Но это мы нашли интервальную оценку для среднего квадратического отклонения .Теперь, чтобы найти интервальную оценку дисперсии норм-го распределения нужно вычислить корни и все? То есть ответом будет

? Или я не прав?
|
i |
Не нужно создавать несколько веток для одной темы. Ветки соеденены.
/ GAA, 02.05.13 |