Тао сформулировал чистую аналитическую задачу, к которой сводится оптимизация Жанга.
This comment is implicit in the above post, but I thought I would highlight it again. Morally speaking, the above analysis shows that the conjecture
![$DHL[k_0,2]$ $DHL[k_0,2]$](https://dxdy-04.korotkov.co.uk/f/3/2/5/3256eee7ae269d4a0b60d2bac90e9f1782.png)
will hold for any natural number
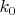
for which one can find a smooth function
![$g: [0,1] \to {\bf R}^+$ $g: [0,1] \to {\bf R}^+$](https://dxdy-02.korotkov.co.uk/f/9/4/e/94ec196405e44d9f5d7c4ae62b91dd8a82.png)
vanishing to order at least
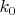
at 1 for which the inequality
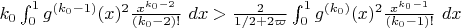
holds (with
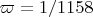
), or equivalently if there exists a smooth function
![$ f: [0,1] \to {\bf R}^+$ $ f: [0,1] \to {\bf R}^+$](https://dxdy-03.korotkov.co.uk/f/e/1/e/e1e9c07053747d8f22855c645763ef7182.png)
with
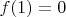
such that the inequality
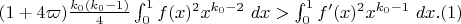
(This is cheating a little bit because there is also an error term \kappa in the analysis, but this term is exponentially small and is basically negligible for the purposes of optimising
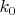
.)
Finding the optimal value of
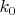
for which this inequality (1) holds is a calculus of variations / numerical spectral theory / ODE problem which appears to be quite computationally tractable. Right now we can obtain the value
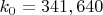
just by substituting in monomials
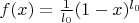
, but these are not the optimal solutions and one should be able to do better, thus improving
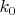
and hence the bound H on the gap between primes