Доброго Времени Суток!
При решении уравнений движения ракеты возникли сложности с решением системы.
Для начала привожу необходимые формулы и уравнения.
В переделах активного участка

-ой ступени пакеты интегрирование системы уравнений удобнее производить по аргументу
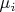
, который связан со временем полета ракеты следующим соотношением:

где:

- средний секундный расход топлива при работе двигателей

-ой ступени;

- текущее значение времени с момента старта (есть величина шага интегрирования);

- момент выключения двигателей

-й ступени. Для первой ступени

;

- начальная масса

-й ступени.
Приведем уравнения движения на активном участке траектории для первой ступени.
Зададимся вспомогательными коэффициентами:
![$$A_1 = \frac {g_0} {1-\mu_1}(P_{sp}^{sl} + (P_{sp}^v - P_{sp}^{sl})[1-\frac {p_h}{101360}])$$ $$A_1 = \frac {g_0} {1-\mu_1}(P_{sp}^{sl} + (P_{sp}^v - P_{sp}^{sl})[1-\frac {p_h}{101360}])$$](https://dxdy-04.korotkov.co.uk/f/7/0/9/7093aaf3557cbb757deae7778db8ede982.png)


где:

- ускорение свободного падения;

- Удельный импульс двигателя на уровне земли;

- Удельный импульс двигателя в вакууме;

- плотнось воздуха на высоте

;

- плотность воздуха на уровне земли [н/м2].

- начальная нагрузка на мидель ракеты;

- число Маха.

, где

- текущая скорость,

- скорость звука [м/с];

- начальная тяговооруженность первой ступени.
Тогда система уравнений движения первой ступени примет вид:

где:

- приращение горизонтальной составляющей скорости;

- приращение вертикальной составляющей скорости;

- приращение дальности полета;

- приращение высоты полета;

- скорость полета;

- радиус Земного шара;

- радиус-вектор;

- высота полета;

- угол атаки;

- угол тангажа;

- программа изменения угла тангажа.
Программа изменения угла тангажа следующаяя:

где первый столбец - начало времени, с которой начинается данная строка (секунды с момента старта);
второй столбец - угловая скорость изменения угла тангажа (градусов/сек);
третий столбец - предельный угол тангажа, до которого продолжается изменения в данной строке.

и

- аэродинамические коэффициенты. Задаются зависимостью от числа Маха (т.е. Скорости деленной на скорость звука):


Итак, известна начальная и конечная массы ракеты, удельные импульсы в пустоте и на уровне земли,
массовый расход топлива, зависимости плотности воздуха от высоты, коэффициентов лобового и
бокового сопротивления от скорости, закон изменения угла тангажа.
Вопрос: как мне организовать решение данной системы через EXCEL (задав шаг ингегрирования допустим 0.1 сек)? Возникли сложности с численным решением данной системы. С какого преобразования стоит начать ее решать численно?
Заранее благодарен за ответ!