Рекуррентная последовательность x-1/x

[Alex_J]

Однажды я заинтересовался этой последовательностью, и как начал ее изучать - так становится всё интереснее и интереснее.
Здесь - о результатах и нерешённых задачах. Читать неспешно, за чашкой чая Материал объёмный.

1. Введение
Итак, речь идёт о последовательности (далее П.)

$$x_{n+1}=x_n-\frac{1}{x_n}\eqno(1.1)$$

Сразу пригодится и обратная

$$y_{m+1}=\frac{y_m\pm\sqrt{y_m^2+4}}{2}\eqno(1.2)$$

Индексы n и m очевидно взаимосвязаны - ведут отсчёт в противоположные стороны.

Основная задача: найти явный вид функции от индекса:

$$x_n=x(n) \eqno(1.3a)$$

$$y_m=y(m) \eqno(1.3b)$$

Сразу скажу: задача не решена. Поэтому речь пойдет как о свойствах П., так и о путях поиска явного вида.

Типичное поведение (1.1) показано на рис. 1 ($x_0=1.48775$) и 2 ($x_0=1.48776$).

Рис.1

Рис.2
Сразу видно интересное свойство: поведение очень сильно зависит от начальных данных. Как именно - ниже.

У П. множество интересных свойств, а также несколько путей нахождения явного вида (1.3), обо всём по порядку.

2. Свойства П. (1.1)

Привожу свойства без выводов, в основном всё довольно очевидно (когда уже знаешь ), если есть вопросы - отвечу дополнительно.

[*] Выражение элементов П. через все предыдущие.

$$x_n=x_0-\sum^{n-1}_0{\frac{1}{x_k}}\eqno (2.1)$$

Вспоминая понятие среднего гармонического $G(x_0,...,x_{n-1})$, записываем (2.1) так:

$$x_n=x_0-\frac{n}{G(x_0,...,x_{n-1})}\eqno(2.2)$$

[*] Выражение через непрерывную дробь

$$x_{n-1}=x_n+\frac{1}{x_n+\frac{1}{x_n+\frac{1}{x_n+...}}}\eqno(2.3a)$$

Что в обозначениях обратной П.

$$y_{m+1}=y_m+\frac{1}{y_m+\frac{1}{y_m+\frac{1}{y_m+...}}}\eqno(2.3b)$$

Непрерывные дроби изначально рассматривались с целыми параметрами, но здесь они могут быть вплоть до комплексных, зато одинаковые. Особый случай непрерывной дроби.

Из (2.3) и (1.2) получаем занятное тождество (заменяя $x_n$ на x ввиду ненужности индекса, т.к. выражение получено для любого x):

$$x+\frac{1}{x+\frac{1}{x+\frac{1}{x+...}}}=\frac{x+\sqrt{x^2+4}}{2}\eqno(2.4)$$

Можно построить конечную дробь следующим образом:

$$x_{n}=x_{n-1}-\frac{1}{x_{n-2}-\frac{1}{...-\frac{1}{x_0}}}\eqno(2.5)$$

Приравнивая (2.1) и (2.5), получаем любопытное соотношение для членов П.:

$$x_0-\sum^{n-1}_0{\frac{1}{x_k}}=x_{n-1}-\frac{1}{x_{n-2}-\frac{1}{...-\frac{1}{x_0}}}\eqno(2.6)$$

3. Свойства обратной П. (1.2)
[*] Неоднозначность и ветвление
Как видно из (1.2), каждый раз для любого m мы получаем два m+1-ых значения, каждое из которых, следовательно, при подстановке в (1.1) даёт одно и то же n+1-е значение.
Более того, для любого $x_n$ имеется ровно $2^{n}$ возможных значений $x_0$, дающих на n-й итерации заданное $x_n$.

[*] Собственная последовательность
Очевидно, что, если $x_0=0$, то у (1.1) дальше значения просто отсутствуют. Подставляя $y_0=0$ в (1.2), получаем обратную последовательность, все значения которой таковы, что, будучи подставленными как $x_0$, они порождают П. (1.1) с конечным числом членов, и последний из них равен 0.
Такую обратную П. и соответствующие значения называем собственными или запирающими, а П. (1.1), построенную от этих чисел, также называем конечной.
Обозначаем собственные значения так: $\widetilde{y_m_k}$, где m - индекс обратной П., а k обозначает одно из возможных значений, и $k=1..2^m$. Множество собственных значений пишем буквой $\mathbb{Y}$, а подмножество $\widetilde{y_m_1}..\widetilde{y_m_{2^m}}$ пишем с индексом $\mathbb{Y}_m$.
Строгого правила нумерации на подмножестве $\mathbb{Y}_m$ пока не задаём.

Утверждение (очевидное): $\forall y_0 \forall m>0 \forall k=1..2^m y_m_k\in \mathbb{Y}_m \Leftrightarrow y_0 \in \mathbb{Y}_m$. На словах: нулевое значение собственное тогда и только тогда, когда все m-e значения собственные.

Чему же равны собственные значения:
$y_0=0$; $y_1_1=1$, $y_1_2=-1$; $y_2_1=\varphi=1.618...$, $y_2_2=-\varphi+1=-0.618...$, $y_2_3=-\varphi$, $y_2_4=1-\varphi$. И т.д.
Итак, $\mathbb{Y}_2$ состоит из значений золотого сечения и обратных ему, с разными знаками.

Докажем утверждение об иррациональности всех $\widetilde{y_m_k}$, m>2. Если какое-либо $\widetilde{y_m_{k_i}}$ рационально, т.е. $\widetilde{y_m_{k_i}}=\frac{p}{q}$, p и q натуральные, то соответствующее ему $\widetilde{y_{m-1}_{k_j}}=\frac{p^2-q^2}{pq}$ также рационально, так же как и все последующие, вплоть до $y_2_{k_l}$, и получаем противоречие, т.к. золотое сечение - иррациональное число.

[*] Аттракторы (циклические последовательности)
Это свойство как П. (1.2), так и (1.1).
Имеются такие значения $x_0$, что при некотором n $x_n=x_0$. Это и есть уравнение для их нахождения, а вот результаты интересные.
Для n=1 значений нет (точнее, как бы есть одно: $x_0=x_1=\infty$).
Для n=2 набор значений таков: {$\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}$}. Т.е. при подстановке в $x_0$ любого из этих значений получаем П., состоящую из чередующихся этих же значений.
Для n=3 имеется 6 решений, группирующихся в два аттрактора с противоположными знаками: {1.4619, 0.7779, -0.5077} и {-1.4619, -0.7779, 0.5077}. Легко видеть из (1.1), что для любого $x_0$ П., построенная от $-x_0$, будет вся отличаться знаками. Поэтому, найдя любой аттрактор, мы автоматически знаем и второй - с противоположными знаками.
Для более высоких n вычисление аттракторов можно предложить в качестве упражнения.

Интересен вопрос - какова вероятность, выбрав произвольное $x_0$, "попасть" на некоторый аттрактор. В принципе, она всё-таки нулевая, т.к. множество аттракторов счетно, а множество вещественных чисел - непрерывно. Значит, выбирая произвольное $x_0$, мы наверняка получаем П. с неповторяющимися значениями.

4. Другие представления П.
[*] Рациональное и собственное представления П. (1.1)
Очевидно, что общий вид $x_n$ от $x_0$ - это дробь вида $\frac{P_n}{Q_n}$, где $P_n$ и $Q_n$ - многочлены от $x_0$, причем порядок $P_n$ равен $2^n$, а порядок $Q_n$ равен $2^n-1$.

Так,

$$x_1=\frac{x_0^2-1}{x_0}$$

$$x_2=\frac{x_0^4-3x_0^2+1}{x_0^3-x_0}$$

$$x_3=\frac{x_0^8-7x_0^6+13x_0^4-7x_0^2+1}{x_0^7-4x_0^5+4x_0^3-x_0}$$

Особый интерес представляет задача о нахождении коэффициентов многочленов $P_n$ и $Q_n$ произвольного порядка. Ещё не решена в обход вычисления многочленов через (1.1) .

Разложим теперь на множители эти многочлены. Оказывается, что

$$x_1=\frac{(x_0-1)(x_0+1)}{x_0}$$

$$x_2=\frac{(x_0-\varphi)(x_0+\varphi)(x_0-(\varphi-1))(x_0+(\varphi-1))}{x_0(x_0-1)(x_0+1)}$$

И так далее. Т.е., имеем общую формулу для $x_n$ такую!

$$x_n=\frac{\prod^{2^{n-1}}_{k=0}{(x_0-\widetilde{y_n_k})}}{\prod^{n-1}_{i=0}{\prod^{2^{i-1}}_{j=0}{(x_0-\widetilde{y_i_j})}}}\eqno(4.1)$$

Это подтверждается при проверках. Таким образом, мы получили выражение n-го члена П. через собственные числа! Это и называется собственным представлением.
Это представление наглядно показывает уже упомянутые свойства собственной П. Взглянем в числитель: если $x_0$ равно одному из $\widetilde{y_n_k}$, то $x_n=0$. И взглянем в знаменатель: если $x_0$ равно одному из $\widetilde{y_m_k}$, m<n, то знаменатель обращается в 0, а значит, $x_n$ не определено. Эти свойства были выведены сначала по-другому, но было удивлением увидеть, как прямолинейно и без лишних наворотов они определяют сам вид значений $x_n$.

Сколько ещё интересных фишек хранит в себе объект исследований - только предстоит открыть, кое о чём я скажу далее.

Строковая (двоичная) запись обратной П.
Вспомним выражение (1.2). Мы можем выбирать знак на каждой итерации. Пусть знак, выбираемый на m-й итерации, в общем случае обозначается $\alpha_m$. Обозначим случай $\alpha_m=1$ как "1", а $\alpha_m=-1$ как "0". Тогда мы можем записать последовательность (1.2) как

$$\{y_0,S\}\eqno(4.2)$$

, где S - двоичная строка из единиц и нулей, читаемая и пронумерованная слева направо начиная с 0. Можно сказать, что S - это упорядоченное множество вида $\{S_m=\frac{1+\alpha_m}{2}\}$.

Когда $S_m=1$, значения обратной П. по модулю увеличиваются, когда же $S_m=0$, то обратная П. перепрыгивает через нуль и меняет знак.
Это происходит поскольку $\lvert{y_m}\rvert<\lvert\sqrt{y_m^2+4}\rvert$. При $S_m=0$, $\lvert y_{m+1}\rvert \in (0;1)$, если убрать модуль - знаки у единицы и члена П. противоположные. Это легко проверить.

Таким образом, нуль в S (и знак "-" в (1.2)) отображает всю числовую полупрямую одного знака в интервал $(0;\pm1)$ другого знака. Это пригодится в разделе 6.

! Обратная П. (1.2) с представлением (4.2) и выбором конкретного $y_0$ даёт возможность (при переводе строки S длины m в соответствующее десятичное число) составить (выделить из вещественных чисел) упорядоченное и пронумерованное подмножество "сложновыразимых" иррациональных чисел.

5. Смежные последовательности
Смежными я называю последовательности, получаемые из (1.1) и (1.2) заменой переменных. Тема только начата, поэтому здесь будет пока один подраздел.

[*] Самая простая замена: $t_n=\frac{1}{x_n}$

Здесь получаем интересные результаты.

$$\frac{1}{t_n}=\frac{1}{t_0}-\sum^{n-1}_0 t_k\eqno(5.1)$$

$$t_n=\sum^{2^n -1}_{k=0}\frac{c_n_k}{x_0-\widetilde{y_n_k}}\eqno(5.2)$$

Коэффициенты $c_n_k$ считаются следующим образом:

$$\frac{1}{x_1}=\frac{x_0}{x_0^2 -1}=\frac{c_1_0}{x_0 -1}+\frac{c_1_1}{x_0 +1}$$

Откуда $c_1_0=c_1_1=\frac{1}{2}$, т.е.

$$t_1=\frac{1}{2}\frac{t_0}{1-t_0}+\frac{1}{2}\frac{t_0}{1+t_0}$$

И вообще

$$t_{n+1}=\frac{t_n}{2}(\frac{1}{1-t_n}+\frac{1}{1+t_n})\eqno(5.3)$$

Коэффициенты $c_2_k$ (нумерация по $k$ вообще говоря условна, как и нумерация \widetilde{y_m_k}. Нужно задаться целью составить правило для нумерации, но пока в этом нужды нет. Хотя некоторые варианты довольно очевидны):

$$c_2_0=c_2_1=\frac{5+\sqrt{5}}{320},c_2_2=c_2_3=\frac{5-\sqrt{5}}{320}$$

А вот один из $c_3_k$:

$$c_3_0=\frac{4}{5}\frac{(\sqrt{5}+1)\sqrt{5}}{(1+3\sqrt{5}-\sqrt{22-2\sqrt{5}})(1+3\sqrt{5}+\sqrt{22-2\sqrt{5}})}$$

Коэффициенты $c_n_k$ выражаются через $\widetilde{y_m_k}$, приводить выкладки буду только по запросу, они громоздкие, а для n>2 рекомендуется Maple.
(Правда, Maple не умеет производить вычисления коэффициентов по такому методу. Ему нельзя объяснить, чтобы он приравнял $\frac{x_0}{x_0^2 -1}$ к $\frac{c_1_0}{x_0 -1}+\frac{c_1_1}{x_0 +1}$ и выделил отсюда подходящие $c_n_k$. Приходится это делать вручную.)

6. Итерационные полосы
Можно доказать, что, если для некоторого n $x_n\in\{\widetilde{y_m_k^+};\tilda{y_{m+1}_k^+}\}$, то непременно $x_{n+1}\in\{\widetilde{y_{m-1}_k^+};\widetilde{y_{m}_k^+}\}$. Это означает, что интервал $\mathbb{Y}_m^+$ отображается с помощью (1.1) в $\mathbb{Y}_{m-1}^+$. Можем дополнить интервалы граничными точками - собственными значениями - и утверждение останется верным.

Утверждение: для любого $x_0\neq\widetilde{y_m_k}$ члены $\{x_n\}$ проходят каждую итерационную полосу и не более одного раза подряд. Доказательство простое, приведу по запросу.


Рис. 3 - Итерационные полосы и фрагмент кривой $x(n)$ (на самом деле, точки соединены прямыми, но и искомая функция будет близка к этой кусочно-линейной, о чём ниже)

Рис. 3 иллюстрирует поведение значений П. и характер итерационных полос. Они напоминают уровни энергии в некоторой квантовой яме. Интересно, каков вид потенциала в такой яме?

Индекс по оси абсцисс увеличивается на 1, и каждый раз искомая кривая $x(n)$ пересекает одно из собственных значений.

В принципе, мы могли бы назначить границами итерационных полос любые значения, построенные от некоторого $y_0$ выражением (1.2). Но наиболее естественными для этого являются именно собственные значения.
Это существенное свойство нашей П. Если взять набор значений $y_0$ и от них построить обратные П., то получится семейство непересекающихся кривых (ну или точнее они будут лежать на искомых кривых, и они не пересекаются). Как будет говориться ниже, по сути, это одна и та же кривая, только параллельным переносом по $x$ смещенная в зависимости от $y_0$ (или от $x_0$).

7. Прямые ветви и их длины. Вычисление без итерирования.
Нужно понимать, что выбор знака в (1.2) мы можем делать сами на каждой итерации, но в (1.1) перепрыгивание через нуль происходит только в зависимости от $x_0$, и эта зависимость нетривиальна.
Если мы считаем (1.2) всегда с $\alpha_m=1$, то значение по модулю неограниченно возрастает.

Назовём подмножество, состоящее из $\nu$ штук членов (1.1), идущих подряд с одинаковым знаком, прямой ветвью, а $\nu$ - длиной прямой ветви. Прямая ветвь так названа, чтобы отделить по смыслу от всех "обратных" ветвей, которые можно рассматривать для обратной П. в связи с её разветвлением на каждой итерации.

Зададимся вопросом: как посчитать $\nu$ для заданного $x_0$ без непосредственного итерирования П. (1.1) ?

Очевидно, $\nu$ есть функция от $x_0$. Условие, которое должно выполняться для $\nu$, выглядит так:

$$\begin{cases} sgn(x_{\nu-1})=sgn(x_0)\\ sgn(x_{\nu-1})\neq sgn(x_\nu)\\ \nu=\min\\ \nu>0 \end{cases}$$

Поскольку знак у $x_\nu$ меняется, то при итерировании по окончании ветви для дальнейших расчётов мы полагаем новое $x_0=x_\nu$ и продолжаем итерации до следующей смены знака.
Так мы получаем последовательность длин прямых ветвей $\{\nu_j\}$, которая также поставлена в соответствие значению $x_0$ (не взаимно однозначное).
При построении графика (1.1) первое, что бросается в глаза - это поведение П. (см. рис. 1 и 2): хаотичные перемены знака и сильная зависимость от $x_0$. Поэтому самой интересной задачей, кроме нахождения явного вида от индекса, является также и нахождение последовательности $\{\nu_j\}(x_0)$.

! Эта последовательность является бесконечной при $x_0\neq\widetilde{y_m_k}$, иначе же она конечная, а сумма её членов равна m.

Также $\{\nu_j\}(x_0)$, возможно, апериодична при $x_0$, не входящем ни в один из аттракторов. Это требует выяснения и доказательства.

----
Этот раздел будет завершён позже. Производятся расчёты
----

Если мы проследим "судьбу" значений $x_n$ от конкретного $x_0$, то мы увидим, что, чем ближе $x_0$ к одной из границ своей итерационной полосы, тем и все $x_n$ ближе к своей соответствующей границе, и когда прямая ветвь заканчивается - первое значение следующей ветви тем выше по модулю, чем ближе к нулю последнее значение предыдущей ветви к нулю. Это очевидно из (1.1). Но это и показывает характер и "силу" зависимости всех последующих значений от первоначального. Итерационные полосы уплотняются при увеличении $x$ по модулю, их ширина уменьшается, отсюда и всё бОльшая чувствительность отдалённых значений $x_n$ к начальному.

Если мы рассмотрим обратную П., то мы увидим, что вся числовая полупрямая определённого знака через $S_m=0$ отображается в 0-ю итерационную полосу, затем в 1-ю и так далее. Она отображается во ВСЕ итерационные полосы, и только порядковый номер полосы показывает, через сколько итераций в ходе вычисления П. (1.1) значение "выстрелит" куда-то на полупрямую по ту сторону нуля.

8. Проблемы вычисления П. на компьютере
Точные значения $x_n$ возможны, если $x_0$ рационально. При этом число разрядов в числителе и знаменателе рационального представления $\frac{p}{q}$ каждого следующего члена (после сокращения на общие множители!) растет в 2 раза!

Интересное наблюдение: при таком числе разрядов это взаимно простые числа, иначе бы было возможно дальнейшее сокращение.
Соответственно, растёт как $2^n$ и требуемое количество памяти для хранения чисел, пусть даже в строковом виде.

Если же вычислять в форматах с плавающей точкой, то, очевидно, накапливается ошибка, и интересной задачей является получение оценки этой ошибки в зависимости как от значения $x_0$, так и от числа проведённых итераций. Понятно, что эта ошибка однажды начинает влиять и на длины прямых ветвей, т.е. перескок произойдёт раньше или позже, чем должен, да и вообще с того момента совершенно точно все значения П. будут неактуальны.

Поэтому единственно целесообразным методом вычислений можно считать именно в рациональном представлении.

Вторая часть позже или после первого ответа - форум склеивает сообщения и ограничивает размер одного сообщения.

[gris]

Картинки правда получаются интересными. (Я сразу же поиграл в Эксели).
Такая простая формула, а столько разнообразия. Даже без теории.
Но и теория тоже интересна, конечно. Много вопросов можно исследовать. Что можно будет утверждать о множестве значений последовательности для разных начальных чисел? Ну ясно, что оно не более, чем счётно, но вот что про ограниченность. Ну и так далее.
Надеюсь, что автор не ограничится первыми результатами.

[Alex_J]

9. Наглядно о П. (1.1) и (1.2)

Здесь покажу, как можно построением получать П. (1.1).

[*] Построение П. (1.1)


Рис. 4. Построение П. (1.1)

На числовой прямой выбираем нуль, точку отсчёта. На первом кадре она показана большой точкой.
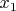
Красная вертикальная полоса на последующих кадрах - это отрезок единичной длины. Она располагается на расстоянии, равном $x_0$ (затем $x_1$ и так далее). Отсчёт всегда идёт от нулевой точки.
Остальное пояснять не буду. На последнем кадре обратите внимание, как получается столь большая величина $\frac{1}{x_n}$, что уходит далеко за пределы изображения и дальнейшее построение уже не показывается.

Вопрос на засыпку: сколько здесь показано перескоков через нуль?

[*] Графики функций $x_n=f(x_0)$
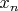
Посмотрим, как выглядят зависимости $x_n$ от $x_0$ для различных n. Это поможет понять, почему столь чувствительны дальние значения к начальным.


Рис. 5а. $y=x_1(x_0)=x-\frac{1}{x}$


Рис. 5б. $y=x_2(x_0)=x-\frac{1}{x}-\frac{1}{x-\frac{1}{x}}$


Рис. 5в. $y=x_3(x_0)=x-\frac{1}{x}-\frac{1}{x-\frac{1}{x}}-\frac{1}{x-\frac{1}{x}-\frac{1}{x-\frac{1}{x}}}$


Рис. 5г. $y=x_4(x_0)=\text{много всего}$

Что мы можем увидеть? Например, что в некотором интервале начинается "каша" из асимптот, и интервал этот ограничивается первыми точками пересечения нуля при приходе графиков из бесконечностей. И эти точки, нетрудно догадаться, равны $x=\pm\widetilde{y_n_k^+}$.
Причём там, среди асимптот, ВСЕ пересечения нуля соответствуют тем или иным собственным значениям.
(Картинки сделаны в Maple. Но она рисует и скачки из + в - на асимптотах, их нужно различать с графиком функции как таковым)

Снаружи же этого интервала четкие асимптоты вида $y=x+c$, что и видно по поведению П. при $x_n\gg 1$.

[*] Построение П. по графику


Рис. 6. Построение П. по графику.

Зелёная линия - это $y=x-\frac{1}{x}$, красная - $y=x$. Начинаем от некоторой точки на прямой и по стрелкам движемся по наглядному алгоритму. Видно, как мы совершаем несколько прыжков через нуль а затем выскакиваем далеко в окрестность -10 и затем долго-долго возвращаемся обратно.
Можно так же строить и обратную П. и увидеть, что на каждом шаге есть выбор знака - в какую сторону двигаться дальше.

Пока это все иллюстрации, дальше возможно будут ещё.

10. Сторонние выводы и применения результатов.

Выражение (2.4) даёт нам вычислимую конечную формулу для всех чисел, задаваемых непрерывной дробью с одинаковыми натуральными коэффициентами (если оставаться в рамках традиционного применения непрерывных дробей) и с одинаковыми вещественными и комплексными числами в общем случае.
Ради интереса, обозначив обе части выражения (2.4) как функцию $\kappa(x)=x+\frac{1}{x+\frac{1}{x+\frac{1}{x+...}}}=\frac{x\pm\sqrt{x^2+4}}{2}$, получим несколько значений:
$\kappa(1)=\varphi=1.618...$ - для напоминания, ну и с единицей это уже известное в математике разложение. Далее,
$\kappa(2)=1+\sqrt{2}$
$\kappa(3)=\frac{3+\sqrt{13}}{2}$
И т.д.
Можно отсюда получить интересные выражения для некоторых корней целых чисел, не являющихся квадратами:
$\sqrt{2}=1+\frac{1}{2+\frac{1}{2+\frac{1}{2+...}}}$ тоже известное представление, зато мы видим как легко оно получается.
$\sqrt{13}=3+2\frac{1}{3+\frac{1}{3+\frac{1}{3+...}}}$
$\sqrt{20}=4+2\frac{1}{4+\frac{1}{4+\frac{1}{4+...}}}$
$\sqrt{5}=2+\frac{1}{4+\frac{1}{4+\frac{1}{4+...}}}=1+2\frac{1}{1+\frac{1}{1+\frac{1}{1+...}}}$
$\sqrt{29}=5+2\frac{1}{5+\frac{1}{5+\frac{1}{5+...}}}$
$\sqrt{10}=3+\frac{1}{6+\frac{1}{6+\frac{1}{6+...}}}$
$\sqrt{53}=7+2\frac{1}{7+\frac{1}{7+\frac{1}{7+...}}}$
Ну и т.д.


А теперь посмотрим на пути поиска явного вида x(n) и y(m).

Поиск явного вида функций от индексов для П. (1.1) и (1.2)

11. Ряды Тейлора и дифференциальные уравнения

Будем искать $x(n)$ в виде

$$x_n=x(n)=\sum^\infty_{i=0}{\frac{a_i n^i}{i!}}\eqno (11.1)$$

где n - вообще говоря, необязательно должно быть целым числом, может быть и вещественным.
Имеет место вот такая любопытная штука. Для всякой хорошей функции f(x) можно представить f(x+a) следующим образом:

$$f(x+a)=\sum^\infty_{n=0}{\frac{f^{(n)}(x)}{n!}a^n}\eqno (11.2)$$

где $f^{(n)}$ суть n-я производная. Т.е. разложение мы делаем по $a$, как по переменному параметру, что вполне справедливо.
В (11.2) мы абстрагировались от прежних обозначений, но далее будем строго их придерживаться.
Используя (11.2), переписываем (1.1):

$$x(n+1)=x(n)-\frac{1}{x(n)}=\sum^\infty_{k=0}{\frac{x^{(k)}(n)}{k!}}\eqno(11.3)$$

Теперь нужно подставить (11.1) в (11.3). Сделаем это неспешно. Запишем выражение для j-й производной от (11.1):

$$x^{(j)}(n)=\sum^\infty_{i=0}{\frac{a_{i+j}n^j}{i!}}\eqno(11.4)$$

Подставляем в (11.3):

$$\sum^\infty_{k=0}{\frac{x^{(k)}(n)}{k!}}=\sum^\infty_{i=0}\sum^\infty_{k=0}\frac{a_{k+i}}{k!i!}n^i\eqno(11.5)$$

Поскольку $x(n+1)$ мы можем так же легко разложить в ряд Тейлора, то

$$x(n+1)=\sum^\infty_{k=0}\frac{a_k (n+1)^k}{k!}=\sum^\infty_{k=0}\sum^k_{i=0}C^k_i \frac{a_k n^i}{k!}=\sum^\infty_{k=0}\sum^k_{i=0} \frac{a_k n^i}{i!(k-i)!}\eqno(11.6)$$

$C^k_i$ - биноминальные коэффициенты. Теперь хотелось бы выделить коэффициенты при $n^i$. Опускаю выкладки, результат таков:

$$x(n+1)=\sum^\infty_{i=0}A_i n^i = \sum^\infty_{i=0}\sum^\infty_{k=i} \frac{a_k n^i}{i!(k-i)!}=\sum^\infty_{i=0}\sum^\infty_{k=0} \frac{a_{k+i}}{k!i!}n^i\eqno(11.7)$$

! Мы получили интересное равенство для коэффициентов ряда Тейлора вида (11.1) для функции $x(n+1)$:

$$A_i=\sum^\infty_{s=i}\frac{a_s}{i!(s-i)!}=\sum^\infty_{k=0}\frac{a_{k+i}}{k!i!}\eqno (11.8)$$

Представим (1.1) в виде

$$x^2 (n)-x(n+1)x(n)=1\eqno(11.9)$$

И перейдём к представлению в виде сумм:

$$\sum^\infty_{i=0} \sum^\infty_{j=0} a_i(a_j-A_j)n^{i+j}=1 \eqno (11.10)$$

Каждое слагаемое приводим к удобному виду.

$$\sum^\infty_{i=0} \sum^\infty_{j=0}a_i a_j n^{i+j}=\sum^\infty_{i=0} \sum^i_{j=0}a_i a_{i-j}n^i = \sum^\infty_{i=0}R_i n^i\eqno (11.11)$$

$$\sum^\infty_{i=0} \sum^\infty_{j=0}a_i A_j n^{i+j}=\sum^\infty_{i=0} \sum^\infty_{j=0}\sum^\infty_{k=0}\frac{a_i a_{k+j}}{k!j!}n^{i+j}=\sum^\infty_{i=0} \sum^i_{j=0}\sum^\infty_{k=0}\frac{a_j a_{k+j}}{k!j!}n^i=\sum^\infty_{i=0}S_i n^i \eqno (11.12)$$

И получаем краткую запись уравнения (1.1) в виде суммы:

$$\sum^\infty_{i=0}(R_i-S_i)n^i=1 \eqno (11.13)$$

Т.е.

$$R_i-S_i=\delta_i=\begin{cases} 0, i\neq 0\\ 1, i=0 \end{cases}\eqno(11.14)$$

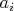
Система уравнений (11.14) - шаг к получению коэффициентов $a_i$ явного представления последовательности (1.1). Так и назовём её системой уравнений явного вида. В развёрнутом виде она выглядит так:

$$\sum^i_{j=0}a_i a_{i-j}-\sum^i_{j=0}\sum^\infty_{k=0}\frac{a_j a_{k+j}}{k!j!}=\begin{cases} 0, i\neq 0\\ 1, i=0 \end{cases}\eqno(11.15)$$

На этом путь поиска явного вида этим способом пока останавливается. Решение систем линейных уравнений с бесконечным числом слагаемых - сама по себе интересная задачка, и, кроме того, здесь, вероятно, снова произойдёт переход к рекуррентным соотношениям коэффициентов.

12. Производящая функция.
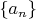
Производящей функцией последовательности $\{a_n\}$ называется функция вида

$$G(z)=a_0+\sum^\infty_{n=1}a_n z^n\eqno (12.1)$$

которую в случае линейных рекуррентных последовательностей нетрудно найти и с её помощью получить явное выражение для $a_n=a(n)$.
Попробуем этот способ для нашей П. (1.1).

$$G(z)=x_0+\sum^\infty_{n=1}(x_{n-1}-\frac{1}{x_{n-1}})z^n=x_0+z\sum^\infty_{n=0}(x_n-\frac{1}{x_n})z^n\eqno(12.2)$$

Т.к. $G(z)=\sum x_n z^n$, то получаем уравнение:

$$G(z)=x_0+z G(z) - z F(z)\eqno(12.3)$$

где $F(z)=\sum^\infty_{n=0}\frac{z^n}{x_n}$. Чтобы получить в правом слагаемом $G(z)$, введём свёртку $A(z)=F(z)G(z)$ и тогда имеем:

$$G(z)=x_0+z G(z) - \frac{z A(z)}{G(z)}\eqno(12.4)$$

Откуда

$$G(z)=\frac{-x_0\pm\sqrt{x_0^2+4z A(z)(z-1)}}{2(z-1)}\eqno(12.5)$$

Теперь распишем $A(z)$:

$$A(z)=F(z)G(z)=\sum^\infty_{n=0}\frac{z^n}{x_n}\sum^\infty_{n=0}x_n z^n=\sum^\infty_{n=0}z^n\sum^n_{i=0}\frac{x_i}{x_{n-i}}\eqno(12.6)$$

Теперь введём обозначение для $a_n$:

$$A(z)=\sum^\infty_0 a_n z^n$$

$$a_n=\sum^n_{i=0}\frac{x_i}{x_{n-i}}$$

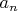
Очевидно, что $a_0=1$, остальные же коэффициенты требуют рекуррентного подхода к вычислению, что приводит по сути к исходной задаче. Присутствие в выражениях самих членов П. не приводит к восторгу.

13. Непрерывные отображения
И вот в итоге к чему приходим.
Если посмотреть на график П. свежим взглядом, то есть смысл задаться следующим вопросом.

Мы испробовали напрашивавшиеся способы решения задачи без вникания в то, какое же именно решение нам нужно.
В соседней ветке про вложенные функции участники говорили, что, имея рекуррентную последовательность, мы можем задать такую функцию, что она принимает нужные нам значения в известных точках а между ними ведёт себя произвольным образом.

Но самый простой вариант, который позволяет нам наложить очень жёсткие требования на конкретное решение, сам напрашивается из графика. Соединяем точки самой плавной линией, какую только интуитивно представляем себе. И задаёмся вопросом: а как она должна себя вести?

И тут начинается самое интересное, что уводит в совершенно особенную сферу. Но об этом - ниже и не здесь.

А пока посмотрим ещё раз на мысленную линию, плавно соединяющую точки, например те точки, которые находятся на рис. 1 и 2. Возьмём пока что только одну прямую ветвь, вообще любую, но одну, без включения перескока через нуль. Для простоты. Потому что там, где перескок, явно происходит что-то, возможна асимптота - и из наших нижеследующих требований на функцию, очевидно, так оно и есть.

Итак, раз мы взяли одну ветвь, то:
1) на ней наша функция монотонна.
2) она нигде не постоянна.
3) она либо положительна, либо отрицательна (не берём нуль в область значений).
4) исходя из условия всей задачи, аргумент функции определяется довольно специфически, а именно: мы ведь выбираем произвольное $x_0$ для рассуждений и вычислений, а это значит, что в $x(n+c)$ мы сами выбираем константу $c$. Что это значит, мы вероятно поймём позже.
5) Все ветви ведут себя одинаково. То есть, все прямой ветви - это обрезанные клоны одной бесконечной (обратной, с т.з. её построения) ветви с $x_0=\infty$ (как бы бесконечности, точнее сколь угодно большому числу). После перескока отсчёт прямой ветви начинается с какого-то места, зависящего от конца предыдущей прямой ветви.

Пункт 5 означает, что функция эта вполне конкретная, что дискретным образом устанавливаемые значения лишь "скользят" по ней в зависимости от выбора $x_0$. Теперь нам нужно перевести вот это интуитивное понимание на язык математики и теперь уже именно отсюда вытащить решение задачи.

Такой выбор функции даёт нам возможность утверждать следующее.
1) Если бы мы взялись посчитать $x(n+\alpha)$, где $\alpha\in(0;1)$, то (здесь и далее рассматриваем случай $x_0>0$, если нужно - все знаки меняются на обратные. Соответственно, функция либо монотонно убывает при $x_0>0$, либо монотонно возрастает) $x(n+1)<x(n+\alpha)<x(n)$ - в силу монотонности
2) Поскольку мы выделили ветвь как повторяющееся в силу дискретности рекуррентной последовательности множество, но видим, что это "след" конкретной функции, то теперь ясно, что аргумент этой функции ограничен сверху, что функция всё-таки должна пересекать нуль и давать, скорее всего, вертикальную асимптоту а затем обрыв.
3) $x(n+\alpha)=x(n+\alpha-1)-\frac{1}{x(n+\alpha-1)}$ - поначалу это наше требование, но теперь оно настолько очевидно, что едва ли нуждается в пояснениях. Здесь как-то по едва уловимым аналогиям можно вспомнить итерационные полосы. И если мы "скользим" конструкцией из этих двух точек, $x(n+\alpha-1)$ и $x(n+\alpha)$ вдоль нашей функции, то мы "получаем" опять же вполне хорошую, монотонную функцию, возможно даже, с минимальной из возможных длиной своей кривой, из всех кривых, какие только можно построить по энному количеству точек. Хороший критерий, кстати. Почти как принцип наименьшего действия.

В самом деле, мы произвольны в выборе $x(0)$, и если мы выбираем некоторое $x(0)$ и получаем $x(1)=x(0)-\frac{1}{x(0)}$, то, зная эти значения, мы можем выбрать некое новое $x'(0)\in(x(0);x(1))$ и получить $x'(1)$ в некотором смысле в том же месте относительно $x(1)$ и $x(2)$, что и $x'(0)$ - относительно $x(0)$ и $x(1)$.

Вот теперь, хорошо представляя себе, что мы хотим получить, формализуем задачу и переводим её на строгий язык так, как только это возможно.


Отступление от темы.
Вообще говоря, есть простой способ получения функции по известным точкам. Например, если нам дан набор аргументов $(x_1,x_2,...,x_n)$ и соответствующих значений $(y_1,y_2,...,y_n)$, то самая простая функция, проходящая через точки $(x_k,y_k)$, выглядит так:

$$y(x)=\sum^n_{j=1}y_j\frac{\prod^{n,i\neq j}_{i=1}(x-x_i)}{\prod^{n,i\neq j}_{i=1}(x_j-x_i)}$$

Но во-первых у нас может быть бесконечное число точек, во-вторых мы не хотим привязываться к значениям самой П., т.к. их все нужно вычислять через итерации, а как раз от этого мы хотим уйти. И в-третьих, получается некий многочлен, скорее всего очень сильно "дрыгающийся" и "пролетающий" на всех парах наши точки с большими значениями первой производной. Что совсем не похоже на ту гладкую и плавную функцию, которую мы хотим построить.

Проблема в том, что мы интуитивно-то понимаем, что плавное изменение начального значения приводит и к плавному изменению всех членов П., и это может выглядеть как раз как "скольжение" точек П. по искомой кривой. Но мы при этом не знаем в точности ту меру изменения аргумента $n$ (уже на вещественном множестве), при которой на конкретную величину меняется каждый член П.

Иными словами, пока мы не знаем вида кривой между целочисленными значениями аргумента, мы не можем и сказать, на сколько, например, нужно увеличить $x_0$, чтобы оказаться ровно посередине между n=0 и n=1. Что-то нащупывается, представляется, но пока смутно. Продолжим искать ответ.

Итак, мы сделали вывод, что поведение значений функции таково, что, где бы мы ни взяли начальное значение, следующее должно вести себя по выражению (1.1). Назовём это свойством переносимости аргумента. (то, что выше я назвал "скольжением")
Довольно очевидно, что $\forall k$ $x(k)=f(x(0))$ ведёт себя так же (обладает свойством переносимости аргумента), а $f$ - любое удобное из упомянутых в самом начале выражений для k-го члена через 0-й. Иными словами, и при $\alpha\in(0;1)$ $x(k+\alpha)=f(x(\alpha))$. Таково наше требование на искомую функцию $x(n)$.
Обозначим временно как f(x) выражение для $x(k)=f(x(0))$, $k>0$, и как g(x) выражение для $x(2k)=g(x(0))$. Очевидно, что $x(2k)=f(x(k))=f(f(x(0)))$.
Вот они, вложенные функции снова появились на горизонте.
$g(x)=f(f(x))$. Это свойство вполне естественно для рекуррентной последовательности, для целых k.
Но что если нам распространить это свойство не только на целые k ?
Вполне естественно потребовать, чтобы $x(1)=f(x(\frac{1}{2}))=f(f(x(0)))$, где f(x) переобозначена, т.е. не та же, что выше. И $x(\frac{1}{2})=f(x(0))$ или, в обозначениях П., $x_\frac{1}{2}=f(x_0)$.
Очевидно, что функция должна быть одинаковой для любого $x_0$ (свойство переносимости аргумента).
Смысл таков: существует функция, позволяющая построить новую последовательность, расширив нашу П. в два раза, вставив промежуточные значения между каждыми соседними по приведёному выше правилу.
Или в 3 раза, вставив по 2 промежуточных значения.
Или вообще,
$\forall k>0 \exists \gamma_k(x) : \forall x_0$ $x_1=\gamma_k(\gamma_k(...(x_0)))$, k раз.
Выше мы два раза использовали обозначение $f(x)$ по-разному, сейчас же остановимся на определении $f(x)=x-\frac{1}{x}$.
$\gamma_1(x)\equiv f(x)$
Здесь я останавливаюсь и несколько позже дам ссылку на отдельную тему, посвящённую этому вопросу.

14. Подбор решения.
Это, конечно, самый нестрогий способ, самый интуитивный.
Действовать можно через замену переменных, через подбор по внешнему виду функции, через анализ её поведения, асимптот и т.д.

Логарифм не подходит. Может подойти что-то наподобие самой функции $x-\frac{1}{x}$, но, похоже, асимптотику на бесконечности так просто не выявить.

Вопрос остаётся открытым, раздел - не завершённым.

P.S. Дипломная работа - самая интересная часть обучения, если там есть задание на самостоятельное исследование какого-либо явления или объекта. Такие задания должны быть не только на дипломе, но и в течение всего обучения, начиная со школы. Самым творческим заданием в школе было написание докладов - переписывание уже написанного своими словами - ну и сочинения (впрочем я их терпеть не мог).
Сегодня и доклады, и сочинения можно скачать из интернета, поэтому ценность имеют только уникальные иследования, не имеющие аналогов. Чтобы неоткуда было содрать, если речь идёт о получении оценки за работу.

Нет, это исследование - не дипломная работа. Это скорее восполнение нехватки творческих заданий во время учёбы, хотя, конечно, целью это не ставилось.
Когда каждый учащийся будет проводить, и не по одному, а десятками подобные исследования, по глубине и дотошности, то уровень образования у нас превысит даже доперестроечный. Правда, и система оценок тогда нужна другая. Но это лирическое отступление.

[Alex_J]

На рис. 5б-5г фишка: пересечения кривых с $y=x$ происходят как раз в точках значений аттракторов.
Вот такой простой геометрический способ нахождения этих значений.

gris
благодарю за отзыв и за техническую возможность разместить вторую часть. ))

[Alex_J]

В разделе 13 я обещал дать ссылку на новую тему для развития способа нахождения явного вида (1.3). Вот она:
Преобразование произвольного порядка

Научившись составлять преобразование произвольной меры, мы сможем перейти от $x_1=f(x_0)$ к $x(n)$. Хотя это будет всё ещё нетривиальный поворот мозгов

[Alextp]

Думаю область значений неограничена. почему? потому что задаем начальный $x_0>0$, идет спуск. этот спуск может длиться вплоть до очень маленьких положительных $x_k$, например до $x_k \approx 10^{-5}$ , после чего идет вычисление $x_{k+1} \approx -10^5$ . вот и большое отрицательное значение. чем ближе к нулю, тем больший по модулю след. член.

для каких-то специальных $x_0$ может и получится ограниченная область значений.

[Alex_J]

Alextp

Да, значения любые $(-\infty;\infty)$, иного и не утверждалось, кроме особенностей с собственными значениями.

Всё это уже написано, что вы нового заметили? Может я не разглядел, поясните.

Да, чем ближе к нулю, тем дальше оно затем скачет.

Вот лучше посчитайте, при какой погрешности задания $x_0$ мы получим длину первой прямой ветви с погрешностью больше единицы?

[Alextp]

Я прочитал не все, видимо повторил вас.

- при какой погрешности задания $x_0$ мы получим длину первой прямой ветви

А это вообще можно посчитать? представьте себе большое $x_0 = 100$, и прикиньте длину ветви от такого числа. Возможны оч большие значения, и без итерирования и ПК тут, думаю, не посчитать, если только не удастся вывести приближение какой-то хорощей ф-цией. а его вывести не удастся.

[Alex_J]

Alextp, да всё решаемо.

Раздел 7. Длина прямой ветви (дополнение)

Чтобы приблизиться к вычислению длины прямой ветви $\nu$, рассмотрим некие $x_{0}$ и $x_{k}$ такие, что $x_{0}>1$, $x_{k}>1$, $x_{0}-x_{k}=a>0$. Из (1.1) следует, что количество итераций, требуемых для достижения или пересечения $x_{k}$, может быть оценена, вообще говоря, как величина, прямо пропорциональная разнице между $x_{0}$ и $x_{k}$ и обратно пропорциональная величине шага итерации (приращению значений последовательности) $\frac{1}{\frac{1}{\Delta x}}=\Delta x$. Приращение (по модулю, т.е. мы помним, что значения убывают) в любом случае ограничено $\frac{1}{x_{0}}$ и $\frac{1}{x_{k}}$, поскольку при $x=x_{0}$ приращение равно $\frac{1}{x_{0}}$, а при $x=x_{k}$ оно равно $\frac{1}{x_{k}}$, и не может выходить за эти пределы. В течение нескольких (а именно, $k$) итераций приращение изменяется от $\frac{1}{x_{0}}$ до $\frac{1}{x_{k}}$.

Следовательно, поскольку за $k$ итераций значение меняется от $x_{0}$ до $x_{k}$ (точнее, до некоторой окрестности $x_{k}$) с шагом от $\frac{1}{x_{0}}$ до $\frac{1}{x_{k}}$, имеем оценку $k$:

$$ax_{0}\geq k\geq ax_{k}\eqno(7.1)$$

В самом деле, если шагов менее $ax_{k}$, скажем $ax_{k}-1$, то даже при максимальном шаге $\frac{1}{x_{k}}$ имеем
$x_{0}-\frac{ax_{k}-1}{x_{k}}>x_{k}$
Пусть не так: $x_{0}-\frac{ax_{k}-1}{x_{k}}\leq x_{k}$, $x_{0}x_{k}-x_{k}^{2}\leq ax_{k}-1$, $a\geq\frac{1}{x_{k}}+x_{0}-x_{k}=\frac{1}{x_{k}}+a$, противоречие.

Точно так же, если шагов больше чем $ax_{0}$, скажем $ax_{0}+1$, то при минимальном шаге $\frac{1}{x_{0}}$ имеем $x_{0}-\frac{ax_{0}+1}{x_{0}}<x_{k}$.
Пусть не так: $x_{0}-\frac{ax_{0}+1}{x_{0}}\geq x_{k}$, $x_{0}^{2}-x_{0}x_{k}\geq ax_{0}+1$, $a\leq x_{0}-x_{k}-\frac{1}{x_{0}}=a-\frac{1}{x_{0}}$, противоречие.

Пусть $K_{1}=ax_{0}$, $K_{2}=ax_{k}$ - это крайние значения для числа итераций $k$, и т.к. $x_{0}>x_{k}$, то $K_{1}>K_{2}$.

$$K_{1}-K_{2}=a(x_{0}-x_{k})=a^{2}\eqno(7.2)$$

Максимальное и минимальное числа итераций, которыми ограничено $k$ , различаются на квадрат разницы между $x_{0}$ и $x_{k}$ $^*$ . При $a=1$, $K_{1}-K_{2}=1$. А значит, либо $k=K_{1}$, либо $k=K_{2}$.

$^*$ - вообще говоря, это невозможно, поскольку при любом $x_{0}$ кроме $1$ в последовательности может быть лишь одно целое число. Подразумеваем, что $K_{1}-K_{2}$ может быть лишь приближенно оценено как $a^{2}$. И мы задаёмся вопросом о достижении членами последовательности некоторой окрестности рассматриваемого значения. Например, при $x_{0}=11$, $x_{10}\approx10$.

Длина прямой ветви $\nu$, таким образом, может быть оценена так: перед сменой знака $x_{k}\in(0;1)$, $a\in(x_{0}-1;x_{0})$ и $k\in[1;x_{0}^{2}]$, т.е. мы получили ограничение сверху:

$$\nu\leq x_{0}^{2}\eqno(7.3)$$

Это также косвенно даёт ограничение на функцию $x(n)$, а именно

$$x(n)\leq\sqrt{x_{0}^{2}-n}\eqno(7.4)$$

[Alex_J]

С помощью производящей функции всё-таки можно прийти к некоторым результатам. Но это требует времени, а пока я получил несколько результатов для линейных рекуррентных последовательностей 1го порядка.

Для

$$a_{n}=\alpha a_{n-1}+\beta$$

Явный вид через производящую функцию получен следующий:

$$a(n)=a_0\alpha^n+\beta\frac{1-\alpha^n}{1-\alpha}$$

При $\alpha=0$

$$a(n)=a_0+\beta n$$

Для

$$a_{n}=\alpha a_{n-1}+\beta+\gamma n$$

Явный вид

$$a(n)=\frac{(a_0(1-\alpha)^2+\alpha(\beta+\gamma)-\beta)\alpha^n-\gamma n (\alpha-1)+\beta-\alpha(\beta+\gamma)}{(1-\alpha)^2}$$

[eugrita]

Я конечно ценю стремление математиков да и прочих поиграться в математические игрушечки. Да, много разнообразия скурпулезности. Однако основной вопрос
В какой области техники применяются или могли бы применяться нелинейные возвратные (рекуррентные) последовательности???
Если бы была линейной -еще можно было бы кивнуть в сторону цифровых рекурсивных фильтров. А эта для чего?
(аналогичные вопросы задаю сам себе в других разделах математики например
в теме случайные блуждания с несколькими вариантами выбора - где кроме игр.)

[arseniiv]

eugrita в сообщении #897115 писал(а):

Если бы была линейной -еще можно было бы кивнуть в сторону цифровых рекурсивных фильтров.

А чем нелинейные туда не годятся-то?

[ewert]

Alex_J в сообщении #715421 писал(а):

Для

$$a_{n}=\alpha a_{n-1}+\beta$$

Явный вид через производящую функцию получен следующий:

$$a(n)=a_0\alpha^n+\beta\frac{1-\alpha^n}{1-\alpha}$$

А причём тут вообще производящие функции? Общее решение уравнения есть $a_n=C\alpha^n+\dfrac{\beta}{1-\alpha}$, где произвольная постоянная $C$ определяется из начального условия: $C=a_0-\dfrac{\beta}{1-\alpha}$.

[cooper]

Может автору топика поможет факт. что исследуемую функцию можно представить в виде:
$2\ctg(2\arcctg(x))$ ?

[cooper]

Если сделать следующую замену:

$x = \frac{(t^2-1) + \sqrt{t^4+14t^2+1}}{4t}}$

мы преобразуем исследуемую ф-цию к в следующему виду

$\frac{1}{2}(t-1/t)$, что тождественно равно $\ctg(2\arcctg(t))$,

А данная функция прекрасно сворачивается при последовательных итерациях, и задача сводится к анализу остатков от деления степеней двойки на $\pi$. Насколько я понимаю, как раз при остатках близких к нулю и происходит все самое интересное.