Предпосылки этой темы находятся в теме "Последовательность x-1/x".
Есть функция, задающая рекуррентную последовательность

По сути, рекуррентная последовательность может иметь смысл пошагового преобразования, отображающего R в R. В соседней теме всячески рассматривалась

.
Мы можем также рассматривать более "широкие" шаги, например

, ...,

k раз.
Но мы можем рассматривать и такие преобразования

, что

, или

, или

.
Введём обозначение

вместо

и

в том смысле, в каком они применялись выше, будем называть

порядком преобразования, а для первого порядка пусть будет обозначение

.
Будем записывать функции

как операторы, чтобы избегать нагромождения скобок, подразумевая поначалу, что очередность применения операторов такова, что достаточно добавить скобки, чтобы понять, как их применять и вычислять. Т.е.

и мы опускаем аргумент после правого оператора, подразумевая, что он здесь появляется при записи в виде функции.
Будем обозначать порядок дробным числом, имея в виду, что
![$$\gamma_{\frac{1}{n}}\gamma_{\frac{1}{n}}...\gamma_{\frac{1}{n}}[\text{n раз}]=\gamma_1\eqno(3)$$ $$\gamma_{\frac{1}{n}}\gamma_{\frac{1}{n}}...\gamma_{\frac{1}{n}}[\text{n раз}]=\gamma_1\eqno(3)$$](https://dxdy-01.korotkov.co.uk/f/4/4/c/44c2dd05c9648d7b7724b3c00d44a31782.png)
Мы можем применять вместе операторы любых порядков, подразумевая, что мы понимаем их функциональную запись и её смысл.
Мы также свободны в назначении и переназначении оператора единичного порядка.
В силу этого мы тут же распространяем возможное значение порядка преобразования на рациональные числа. Для этого введём специальное определение:
Под оператором

рационального порядка будем подразумевать оператор, составленный из p операторов порядка

, т.е.
![$$\gamma_{\frac{p}{q}}=\gamma_{\frac{1}{q}}\gamma_{\frac{1}{q}}...\gamma_{\frac{1}{q}}[\text{p раз}]\eqno(4)$$ $$\gamma_{\frac{p}{q}}=\gamma_{\frac{1}{q}}\gamma_{\frac{1}{q}}...\gamma_{\frac{1}{q}}[\text{p раз}]\eqno(4)$$](https://dxdy-04.korotkov.co.uk/f/3/4/d/34d3f1b07e9536437c79f441ba46be2082.png)
Из множества рациональных чисел подтягиваются и все его свойства:
- Коммутативность операторов, а с ним и сложение порядков, которое ассоциируется с умножением операторов, т.е.

Это нужно доказать.
![$\gamma_{\frac{p_1}{q_1}}\gamma_{\frac{p_2}{q_2}}=\gamma_{\frac{p_1 q_2}{q_1 q_2}}\gamma_{\frac{q_1 p_2}{q_1 q_2}}=\gamma_{\frac{1}{q_1 q_2}}\gamma_{\frac{1}{q_1 q_2}}...\gamma_{\frac{1}{q_1 q_2}}[p_1 q_2 \text{раз}]\gamma_{\frac{1}{q_1 q_2}}\gamma_{\frac{1}{q_1 q_2}}...\gamma_{\frac{1}{q_1 q_2}}[p_2 q_1 \text{раз}]=\gamma_{\frac{1}{q_1 q_2}}\gamma_{\frac{1}{q_1 q_2}}...\gamma_{\frac{1}{q_1 q_2}}[p_1 q_2 + p_2 q_1 \text{раз}]=\gamma_{\frac{p_1 q_2 + p_2 q_1}{q_1 q_2}}$ $\gamma_{\frac{p_1}{q_1}}\gamma_{\frac{p_2}{q_2}}=\gamma_{\frac{p_1 q_2}{q_1 q_2}}\gamma_{\frac{q_1 p_2}{q_1 q_2}}=\gamma_{\frac{1}{q_1 q_2}}\gamma_{\frac{1}{q_1 q_2}}...\gamma_{\frac{1}{q_1 q_2}}[p_1 q_2 \text{раз}]\gamma_{\frac{1}{q_1 q_2}}\gamma_{\frac{1}{q_1 q_2}}...\gamma_{\frac{1}{q_1 q_2}}[p_2 q_1 \text{раз}]=\gamma_{\frac{1}{q_1 q_2}}\gamma_{\frac{1}{q_1 q_2}}...\gamma_{\frac{1}{q_1 q_2}}[p_1 q_2 + p_2 q_1 \text{раз}]=\gamma_{\frac{p_1 q_2 + p_2 q_1}{q_1 q_2}}$](https://dxdy-04.korotkov.co.uk/f/3/6/5/365727b8d2cd7ffbfe4025b96ffeb6dc82.png)
А также это равно

, поскольку, приведя к общему знаменателю, мы можем перегруппировать операторы, выделив сначала

штук, а затем

штук.
Тем самым мы доказали коммутативность операторов и применимость к ним сложения порядков.
Вводя обратное преобразование к любому из упомянутых а также нулевое преобразование

, мы разрешаем применять и операцию вычитания.
Таким образом, операторы преобразования

изоморфны множеству рациональных чисел с введённым на нём сложением.
Пример. Параллельный перенос, или функция

- самый простой пример. Очевидно, что

.
Пример на словах. Пусть есть некое отображение множества (пока что подмножества вещественных чисел, а отображение суть функция на нём. Потом расширим понятие) в само себя. Мы задаёмся вопросом: а есть ли преобразование такое, что после его применения n раз мы получим наше исходное преобразование? Ну например 2 раза или 3. А почему бы такое же рассуждение не повторить для этих более "мелкошаговых" операторов и найти между ними промежуточные? И утверждаем, что решение есть (хотя это ещё большой вопрос в конкретных случаях, но вроде бы предпосылок к случаям отсутствия решений пока нет). Но как только мы вводим эти операторы дробного порядка, то тут же открываем для себя все возможности множества рациональных чисел.
Можем ли ввести умножение порядков? Да:

, но нужно понимать смысл этого действия в понятиях операторов. Так, ясно, что умножение порядка на целое число

означает повторение оператора данное число раз. Но деление на целое число

- что это? Наиболее наглядно представить это как "измельчение" оператора, т.е. это уже реально другой оператор, который производит в

раз менее "далёкое" преобразование.
Итак, деление порядков операторов - это порождение более "мелкого", с тем же числом шагов, но не так "далеко" происходящего преобразования.
Здесь уже просто необходимо ввести понятие меры преобразования

.
Мера преобразования  - это то же, что порядок преобразования.
- это то же, что порядок преобразования. Т.е. мы имеем дело с операторами

. Но слово "мера" помогает нам лучше понять смысл этих операторов и ввести
числовую ось меры преобразования.
Пусть дано множество, на котором определена функция

. Исходное состояние множества пусть имеет меру
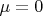
, а после преобразования

приобретает меру, равную

. Тогда, производя повторные преобразования, а также разбивая исходное преобразование на более мелкие и вводя обратные преобразования, мы получаем всю числовую ось меры, по крайней
мере*, для всех её рациональных значений.
* - не без каламбуров.Таким образом, мы получаем возможность работать с отображением множества на себя, как с преобразованием, происходящим столь плавно и столь мелкими шагами, как только мы этого захотим.
Другое дело, что чаще всего
явный вид промежуточных преобразований - это большая загадка. Нахождение их - очень и очень интересная задача.
В самом деле, как например должна выглядеть функция

, если

? Два раза применить это преобразование - и мы получаем синус. Что это вообще за зверь такой? А затем этого зверя мы хотим получить тоже за два шага, и это уже порядок

. И так далее.
На языке уравнений задача выглядит довольно странно: (отходим временно от обозначений гаммами)

А для порядка


А значит

На числовой оси - рисовать не буду - отметьте на отрезке [0;1] точки

,

,

. Вот это те меры преобразования, с которыми мы имеем дело в этом примере.
Между точками

и

напрашивается возможность перехода с помощью ещё более низкого порядка - а именно

:
Пусть

, тогда

Само свойство коммутативности накладывает требование на функции

.
И простейший вид этого требования выглядит так:

И нужно найти не тривиальные решения этого уравнения, да ещё и чтобы получить для единичного порядка исходное преобразование!
Чтобы стало совсем весело, сделаем утверждение:
Порядок преобразования может принимать любые вещественные значения.Его нужно доказывать - раз, понять, что такое преобразование иррационального порядка - два. Но зато это позволит сделать следующий теоретический шаг и ввести...
Бесконечно малое преобразование.Мы действительно можем устремить

к бесконечности в рациональном порядке преобразования

. Почему нет? И где-то там, у пределов нуля, найти бесконечно малое, дифференциальное преобразование

, соответствующее перемещению на оси меры на величину

, с которой, скорее всего, можно работать по всем канонам математики дифференциалов и бесконечно малых величин.
А также мы вводим такое понятие, как плавное преобразование, не как математичекий объект, а больше как умозрительную пока что категорию, которая измеряется мерой

и которая порождает исходное (выбираемое нами) единичное преобразование

при

а также позволяет, выработав методику работы с ним, получать вид преобразования произвольной меры

как значение некоего оператора, который мы назовём...
 - генератор преобразования с мерой
- генератор преобразования с мерой  для исходного преобразования
для исходного преобразования  .
.Это оператор, на входе которого функция и мера, на выходе -

.
Чтобы со всем этим можно было получать реальные результаты, нужно, пожалуй, ввести и найти некое отображение пространства функций f(x) на себя, такое, чтобы операция применения оператора переводилась, например, в перемножение (по аналогии с преобразованием Лапласа, где свёртка через интеграл сводится к умножению), а получение

сводилось, например, к интегрированию генератора

. Хотя, скорее, интегрировать нужно некий дифференциальный генератор.
Итак, пусть существует отображение множества функций на себя

такое, что

, где

- пока что не совсем понятный условный аргумент.





это и есть некий универсальный дифференциальный генератор.

Т.е. мы
1) преобразуем

в её аналог с помощью - назовём его так -
мерного преобразования 
2) берём интеграл от 0 до интересующей нас меры и получаем функцию - генератор гаммы поядка

.
3) Таким образом, генератор, к которому применено обратное мерное преобразование, даёт наше искомое

.
Нарисуем алгоритм решения так:


это прообраз гаммы там, в пространстве генераторов.
Картинка получилась красивая. Теперь осталось самое "малое": адекватно составить мерное преобразование...
Нужно особое внимание уделить переносу функции нулевого порядка

через оператор

.
Предложенный вариант введения мерного преобразования не единственный. Здесь целое поле для экспериментов и исследований. Здесь нужны более точные привязки понятий к множествам, например, с какими множествами можно иметь дело при введении понятия дробного преобразования

для исходного преобразования

. И так далее.......
Начнём
 -- 17.02.2013, 02:39 --
-- 17.02.2013, 02:39 --Да.... самый существенный результат, ради которого и затевалась эта тема, таков:
ведь мера - это полный аналог индекса - аргумента функции явного вида x(n) в теме
Последовательность x-1/x(а точнее, мера

тождественна индексу!!!)
Почему тождественна? Ещё раз проведём рассуждения:
Рекуррентную последовательность

можно рассматривать как отображение R на себя. Мы выбираем любое

и смотрим, что получается, по шагам. Во что преобразуется R. Как там смещаются-перемешиваются исходные значения.
Но сама запись

неизбежнейше наводит на мысль о том, что вот этот индекс

- ни что иное как индекс... нет, не члена последовательности! А шага преобразования множества R !
Что такое

? Это не просто выбранное нами значение. Это ещё и фиксация данного состояния R как исходного. В нём, если бы можно было нумеровать это несчётное множество, каждое значение находится в своей ячейки, т.е. над ним "висит" тождественное преобразование-нумератор:

в

-й ячейке лежит число

. Это
перенумерация после того, как мы, например, получили это значение на 101-м шаге итерации функцией

(и на самом деле наше множество R на этом шаге составлено из значений

,

).
Итак, индекс шага преобразования. Но найдя способ ввести меру преобразования любую, даже рациональную, даже вещественную - мы заложили саму идею того, что индекс может быть промежуточным. И именно

было стартовой идеей, в результате чего мы пришли к мере

, и здесь

.
То есть, мера - и есть индекс. Генератор преобразования

- это и есть то, с помощью чего мы получаем преобразование для произвольного

. Но это пока что лишь функция, от предыдущего значения дающая следующее, пусть и для произвольного индекса.
Когда же мы получим функцию от меры и начального значения - мы заменим меру на индекс и получим явный вид (1.3, тема "x-1/x"). Ну и также, мы научимся переводить любую рекурентную последовательность в явный вид от индекса.