Здравствуйте!
Подскажите пожалуйста, сколькими различными способами можно сконструировать фигуру следующего вида:

Можно переставлять шары с цифрами, но структура должна оставаться.
Мысль такова. Всего перестановок
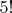
. Повторы могут быть только там, где шар имеет 3 грани, причем именно короткие (третий номер на картинке). Таким образом, фиксируем этот шар (всего 5 вариантов, по количеству номеров) и для каждого номера считаем количество повторов (сочетаний из четырех оставшихся номеров по два), получаем

. Итого

.
Мне кажется, что это слишком много. Спасибо.