1.1. Пусть

,

,

– положительные действительные числа. Докажите, что

1.2.

– точка пересечения диагоналей вписанного четырехугольника

,

– точка пересечения прямых

и

,

– середина стороны

,

– середина стороны

. Окружности, описанные около треугольников

и

, пересекаются во второй раз в точке

. Докажите, что точки

,

,

и

лежат на одной окружности.
1.3. Натуральное число

называется совершенным, если оно равно сумме всех своих натуральных делителей, отличных от самого

. Например, число

– совершенное, поскольку

. Найдите все четные совершенные числа, которые можно представить как сумму двух кубов натуральных чисел.
2.1. Вписанная в равнобедренный треугольник

(

) окружность

касается его сторон

и

в точках

и

соответственно. На продолжении стороны

за точку

выбрана произвольная точка

. Прямая

во второй раз пересекает

в точке

, прямая

во второй раз пересекает

в точке

. На прямой

отмечена такая точка

, что

лежит между

и

,

. Определите геометрическое место точек

.
2.2. В алфавите племени Муму всего две буквы: М и У. Словом в языке Муму является любая последовательность букв М и У, в которой рядом с каждой буквой М есть буква У (например, УУУ и УММУМ являются словами, а ММУ нет). Пусть

обозначает количество слов языка Муму, в которых ровно

букв М и ровно

букв У. Докажите, что

для любых

,

.
2.3. Для натурального числа

обозначим через


-тую цифру слева в десятичной записи числа

(
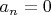
, если в записи числа

меньше

цифр). Рассмотрим бесконечную десятичную дробь

. Докажите, что число

иррационально.
3.1. Найдите все пары взаимно простых натуральных чисел

, которые удовлетворяют равенству

3.2. Расположение

чисел

на окружности назовем

-отрицательным (других чисел на окружности нет). На первом ходу отличник Андрей выбирает одно из чисел на окружности и умножает его на

. Далее на каждом шагу он вместо следующего по часовой стрелке числа на окружности записывает его произведение с числом, записанным на предыдущем шагу. Докажите, что если для некоторого

за

шагов

-отрицательное расположение преобразуется в себя, то за

шагов

-отрицательное расположение также преобразуется в себя.
3.3. Вписанная окружность

треугольника

касается его сторон

,

и

в точках

,

и

соответственно. Пусть

– точка пересечения прямых, проходящих через точки через точки

и

параллельно

и

соответственно,

– основание перпендикуляра, опущенного из точки

на

,

– центроид треугольника

,

– точка пересечения луча

с

. Докажите, что точки

,

и

лежат на одной прямой.
4.1. См.
http://dxdy.ru/topic58039.html 4.2. Пусть

– многочлен с целыми коэффициентами степени

. Для множества

натуральных чисел обозначим

. О натуральных числах

известно, что

. Докажите, что множество

можно разбить на

непересекающихся подмножеств

с одинаковым количеством элементов так, что

.
4.3. См.
http://dxdy.ru/post570048.html#p570048Disclaimer:содержимое взято с сайта http://probability.univ.kiev.ua/userfiles/zhoraster/selection.html с любезного разрешения автора. Дальнейшее воспроизведение условий или их части не разрешено.Поскольку я не смог поставить свое сообщение выше остальных, помещаю условия сюда. Надеюсь, nnosipov не будет возражать  //zhorasterzhoraster
//zhorasterzhoraster, очень любопытно, насколько хорошо участники решали задачу 1 из III-го тура? (Насколько я помню, это слегка отретушированная задача с Питерской олимпиады 2005 года.)
Извиняюсь, не заметил сразу, что там есть и статистика. Да-а, в основном не очень-то справились.