В чём польза континуум гипотезы?

[Борис Лейкин]

Истинна она или ложна в реальном мире, и что?
А с квантовыми компьютерами она случайно не связана?

[Котофеич]

Знаю но не скажу.

[незваный гость]

Ура! мы имеем конечное покрытие! Пространство опроса компактно!

[Brukvalub]

Вот здесь все предельно ясно написано: http://nature.web.ru/db/msg.html?mid=11 ... bruh2.html .

[Котофеич]

А кто такой Калиостро Впервые слышу о таком.

[Brukvalub]

Котофеич писал(а):

:evil: А кто такой Калиостро Впервые слышу о таком.

- это выдуманный персонаж из романа братьев Стругацких "Понедельник начинается в субботу" , этот роман можно прочесть и послушать здесь: http://www.tendresse.ru/luden/a-i-b-str ... v-subbotu/
Еще был граф Калиостро, прародитель сегодняшних жуликов, использующих доверчивость обывателя, он действовал, в частности, в России, см. о нём фильм: http://www.sharereactor.ru/movies/6197

[Котофеич]

Хороший сайтик. Я люблю всякие сказки слушать перед сном. Жалко, что математические сказки пока никто не озвучил. Так оказывается это Калиостро решил
эту задачу Гильберта, а Коэн передрал.

[Mopnex]

Калиостро из братьев Стругацких и из фильма - одно и то же лицо.

[juna]

Борис Лейкин писал(а):

:oops:
Истинна она или ложна в реальном мире, и что?
А с квантовыми компьютерами она случайно не связана?

А мне всегда казалось, что есть некоторая аналогия между евклидовой - неевклидовой геометрией и континуум-гипотезой. И там, и там - полный плюрализм.
И это, как мне кажется, следствие того, что понятие бесконечности существует только в мозгу у человека, в природе (как чувственной данности) ее нет. Поэтому мы можем назначать ей любые свойства, только бы не входить в противоречие с самим собой - природа к этому полностью инвариантна.

[Котофеич]

Mopnex писал(а):

Калиостро из братьев Стругацких и из фильма - одно и то же лицо.

Тогда скорее всего, "Коэн" это просто псевдоним великого мага Калиостро.

[незваный гость]

Да-с, o tempora o mores. Фильм, уж коль на то пошло, был снят по роману А.Н. Толстого «Граф Калиостро». Стругацкие, по-моему, прямо ссылаются на эту книгу. Что же касается исторических сведений, можно что-то найти здесь.

Я не уверен, кстати, что именно эпизод с континиум гипотезой так вдохновил Стругацких. Вряд ли им были неизвестны теоремы Геделя, куда более ранние.

[Борис Лейкин]

Ну, вот же мысля у меня была http://dxdy.ru/viewtopic.php?t=3044:
Если есть квантовые компьютеры экспоненциально эффективнее классических, может есть суперструнные компьютеры экспоненциально эффективнее квантовых? А как насчёт промежуточных по эффективности компьютеров между квантовыми и классическими, а?
http://www.physicsforums.com/archive/index.php/t-125043.html

Цитата:

Континуум-гипотеза: С точностью до эквивалентности, существуют только два типа бесконечных числовых множеств: счётное множество и континуум.

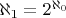
Аналогия вроде есть с мыслью выше? Т.е. классические компьютеры - это счётные множества $\aleph_0$, квантовые компьютеры - континуум $\aleph_1=2^{\aleph_0}$, струнные - $\aleph_2=2^{\aleph_1}$

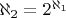
Цитата:

В 1963 году американский математик Паул Коэн доказал, что континуум-гипотезу нельзя ни доказать, ни опровергнуть.

Что это значит? Значит в нашем реальном мире континуум гипотеза может быть как истинной так и ложной, вот я и хотел спросить, что изменится в нашем мире от того так это или нет.

А вот, что говорит Скот Ааронсон:
There actually is a tenuous connection between quantum computing and set theory, which I'll touch on in the next lecture. To give a sneak preview, the connection is that quantum mechanics applied to finite-dimensional systems (like qubits) seems like an interesting "intermediate" case between a continuous and a discrete theory. That is, it involves quantities (the amplitudes) that vary continuously, but that are not directly observable. In this way, it seems to avoid the "paradoxes" associated with the continuum in a way that other continuous physical theories do not.
Т.е. квантовые компьютеры промежуточны между счётным и континуумом. $\exists \mathbb{Q}: \aleph_0 < |\mathbb{Q}| < \aleph_1$
NP-complete Problems and Physical Reality
Can NP-complete problems be solved efficiently in the physical universe? I survey proposals including soap bubbles, protein folding, quantum computing, quantum advice, quantum adiabatic algorithms, quantum-mechanical nonlinearities, hidden variables, relativistic time dilation, analog computing, Malament-Hogarth spacetimes, quantum gravity, closed timelike curves, and "anthropic computing." The section on soap bubbles even includes some "experimental" results. While I do not believe that any of the proposals will let us solve NP-complete problems efficiently, I argue that by studying them, we can learn something not only about computation but also about physics.
S. Aaronson. Is P Versus NP Formally Independent?
This is a survey about the title question, written for people who (like the author) see logic as forbidding, esoteric, and remote from their usual concerns. Beginning with a crash course on Zermelo-Fraenkel set theory, it discusses oracle independence; natural proofs; independence results of Razborov, Raz, DeMillo-Lipton, Sazanov, and others; and obstacles to proving P vs. NP independent of strong logical theories. It ends with some philosophical musings on when one should expect a mathematical question to have a definite answer.

[AlexDem]

Борис Лейкин писал(а):

Континуум-гипотеза: С точностью до эквивалентности, существуют только два типа бесконечных числовых множеств: счётное множество и континуум.

Хм, а эта цитата откуда?

Добавлено спустя 10 минут 29 секунд:

Нашел - из ссылки Brukvalub

[PAV]

Борис Лейкин писал(а):

Цитата:

В 1963 году американский математик Паул Коэн доказал, что континуум-гипотезу нельзя ни доказать, ни опровергнуть.

Что это значит? Значит в нашем реальном мире континуум гипотеза может быть как истинной так и ложной, вот я и хотел спросить, что изменится в нашем мире от того так это или нет.

Континуум-гипотеза не имеет к реальному миру никакого прямого отношения, равно как и подавляющее большинство прочих математических абстрактных построений.

[Борис Лейкин]

PAV писал(а):

Континуум-гипотеза не имеет к реальному миру никакого прямого отношения, равно как и подавляющее большинство прочих математических абстрактных построений.

Вот я и не могу никак понять связь математики и реального мира.
А континуум гипотеза разве не связана с философским (физическим) вопросом о структуре пространства (материи), дискретно оно или непрерывно или может что-нибудь промежуточное между ними?
Ну а непрямое отношение какое-нибудь есть, например, в математике используется же, кажется, как сама КГ так и её отрицание для доказательства каких-то фактов "в анализе, топологии точечных множеств, теории меры", ну, т.е., тогда, КГ имеет отношение не к реальному миру а к его приближениям с помощью математических теорий основанных на разных системах аксиом, как там это обозначается ZF+CH, ZF+(~CH)? (Эх, ну, вобщем, какие приложения континуум-гипотезы в самой математике, я хотел спросить?)