Я точно не знаю, но вот такое нашел:
В Бухштабе есть способ представления числа

квадратичной формой (в том числе формой

), но для его работы надо уметь решать сравнение

. Алгоритм решения сравнений

для простого

есть в Василенко Теоретико-числовые методы в криптографии. Значит, наверное, надо делать так: факторизовать

, затем раскладывать каждое простое в сумму квадратов с помощью решения сравнения в

, а потом разложения комбинировать.
А еще в Гэри Джонсоне я нашел, что к уравнению
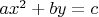
для

сводится задача 3-выполнимости, что не утешает
