Однородное гравитационное поле (поле тяжести) можно получить двумя способами. Первый - введением системы координат, движущейся равноускоренно (по собственному времени) относительно ИСО. Второй - заданием определенной конфигурации тяготеющей материи, при которой пробная частица, под действием сил тяготения, движется по тому же закону.
Думаю, уравнения движения равноускоренной материальной точки и в Ньтоновской механике и в СТО всем известны.
Рассмотрим второй способ.
Известно, что в Ньютоновской механике ему соответствует поле, создаваемое бесконечной материальной плоскостью с постоянной поверхностной плотностью.
Однако, бесконечных материальных плоскостей не существует, поэтому будем считать, что плоскость эта конечна, хоть и очень велика по сравнению с расстоянием до пробной частицы. Простейшее релятивистское обобщение однородного поля тяжести Ньютона :

, где

положительные функции координаты

дают

Теперь вспомним, что гравитационного поля внутри массивной сферы нет (ни в Ньтоновском случае, ни в ОТО). Возьмем такую сферу с постоянной поверхностной плотностью и сделаем в ней прокол, т.е. удалим с поверхности любую гравитирующую точку и поместим ее внутрь сферы в качестве пробного тела.
В виду симметричности ситуации, движение этого пробного тела внутри сферы будет практически эквивалентно движению под действием гравитационного поля, создаваемого материальной плоскостью - касательной к поверхности сферы, расположенной напротив удаленной точки.
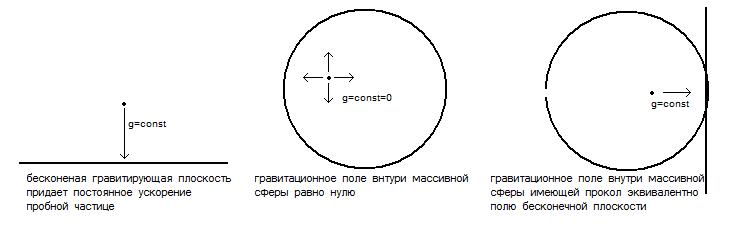
Таким образом, в первом приближении, гравитационное поле внутри массивной проколотой сферы будет однородным, а движение пробного тела равноускоренным.
Этот случай существенно отличается от лифта Эйнштейна, т.к. требуемая "локальность" необходимая для однородности гравитационного поля может иметь космологические масштабы.