Касательно геометрии пространственного трёхмерия в ОТО

[Munin]

Я уже удивился. Вот, значит, до чего может довести введение собственной нестандартной терминологии. Пишете "неинерциальная", а подразумеваете "несинхронизированная"... И это изобретение птичьего языка у вас совместное с zbl и В. Войтик-ом.

Снимаю все свои вопросы и оставляю вас вариться в этом самостоятельно.

Какого бойца мы потеряли...

[Утундрий]

Munin
СО вообще говоря не тождественны СК. Вторых в несколько континуумов больше.

[Joker_vD]

(Оффтоп)

Да приведет ли кто-нибудь когда-нибудь четкое определение СО, СК и в чем они различаются? А то уж пятую тему об десяти страницах читаю, все обвиняют друг друга в незнании этих понятий/неверном использовании, а вот конкретики как-то маловато. Я бы понял, если бы это было "Помогите решить/разобраться (Ф)", там намеки с посланием "да откройте же вы учебник" уместны, но здесь?..

[Утундрий]

Joker_vD в сообщении #512251 писал(а):

Да приведет ли кто-нибудь когда-нибудь четкое определение СО, СК и в чем они различаются?

Коротко говоря, СО это совокупности мировых линий, а все вообще возможные СК факторизуются по отношению сопутствия некоторой СО.

(Оффтоп)

Уже две недели как пытаюсь хотя бы для себя изложить этот вопрос ясно и подробно но пока что все еще не удовлетворен результатом

[Munin]

Утундрий в сообщении #512222 писал(а):

СО вообще говоря не тождественны СК. Вторых в несколько континуумов больше.

Это не мне объясняйте, а вот этим товарищам, пожалуйста. Я уже отчаялся, общаясь с ними, соблюдать правильную терминологию.

Joker_vD
Иваненко, Сарданашвили, Гравитация - Киев, Наукова Думка, 1985.

Цитата:

В предыдущем разделе было отмечено, что «аффинность» пространства Минковского позволяет задать на нем систему координат. На произвольном пространстве одной системы координат, покрывающей все пространство, построить не удается. Однако можно разделить его на области (обычно их конечное число), на каждой из которых такую систему координат ввести можно. Только нужно, чтобы на пересечении областей координатные системы на них были бы согласованы. В таком виде пространство выглядит как бы склеенным из координатных лоскутов.



Формализуем эту наглядную конструкцию. Пусть $U$ — некоторая область пространства $X$ и $\varphi$ — отображение $U$ в некоторую область $n$-мерного вещественного векторного пространства $R^n$ (рис. 8). Тогда всякой точке $x$ из $U$ сопоставим координаты $(x^1,\ldots,x^n)$ вектора $\varphi(x)$ в $R^n$: $\varphi(x)=x^1e_1+\ldots+x^ne_n,$ где $\{e_\mu\}$ — базис $R^n$ подобно тому, как это делалось в пространстве Минковского. Такое сопоставление и называется заданием системы координат (координатной карты) $(x^\mu,U)$ в $U.$
Отображение $\varphi$ и есть та проекция точек пространства $X$ на координатные оси из $R^n,$ о которой мы говорили в предыдущем разделе, давая предварительное определение системы координат.
Склеивание двух пересекающихся карт $(U,x^\mu)$ и $(U',x^{\mu'})$ осуществляется функциями перехода $\varphi'\varphi^{-1}=x^{\mu'}(x^nu),$ $\varphi(\varphi')^{-1} = x^\mu(x^{\nu'}).$ Если эти функции дифференцируемые, то координатные карты называют согласованными, а совокупность всех покрывающих многообразие карт $\Psi_X=\{(U,x^\mu)\}$ — атласом. Задание атласа и означает задание системы координат на многообразии.
На многообразии могут быть заданы различные системы координат. Два атласа $\Psi_X=\{(U,x^\mu)\}$ и $\Psi'_X=\{(U',x^{\mu'})\}$ на многообразии считаются эквивалентными, если любые две пересекающиеся карты $(U,x^\mu)$ из атласа $\Psi_X$ и $(U',x^{\mu'})$ из $\Psi'_X$ согласованы. Переход между эквивалентными атласами — это переход от одной системы координат к другой.
Заметим, что в теории гравитации мы, вообще говоря, не знаем всего многообразия, на котором работаем. Дело в том, что уравнения Эйнштейна и их решения можно рассматривать только отдельно на каждой координатной карте, а сшивать эти карты приходится из каких-либо добавочных соображений, например, учитывая симметрии и др. Поэтому здесь, как правило, имеется определенный произвол.
Рассмотрим теперь важные понятия касательного вектора, касательного пространства, касательного расслоения к многообразию. Подчеркнем, что все конструкции, с которыми мы в дальнейшем встретимся — метрика, связность, кривизна,— определены именно в касательных пространствах.



Строгое математическое определение касательного вектора весьма сложно, поэтому мы будем здесь апеллировать к наглядному представлению о нем как вектора $\tau,$ восстановленного из данной точки $x$ многообразия $X$ касательно к нему (рис. 9). Касательный вектор можно рассматривать также как генератор сдвигов из точки $x$ в направлении $\tau$ и задавать его как оператор дифференцирования $\partial_\tau$ в направлении $\tau.$
Множество всех касательных векторов к многообразию в данной точке $x$ образует касательное пространство $T_x$ к $X$ в точке $x$ (рис. 10).
Касательное пространство $T_x$ является векторным пространством, имеющим ту же размерность, что и многообразие $X^n.$ В качестве базисов пространства $T_x$ удобно выбрать операторы частных производных $\{\partial_\mu\},$ которые являются касательными векторами к проходящим через $x$ координатным линиям (вдоль которых меняется только одна какая-либо координата) некоторой системы координат $\{x^\mu\}.$ Такой базис называется голономным, согласованным с данной системой координат. Однако базис $T_x$ можно выбрать и произвольно, независимо от системы координат.
Задание базиса $T_x$ интерпретируется как задание локальной системы отсчета в точке $x,$ что согласуется с предварительным определением системы отсчета из предыдущего раздела.
Как связаны система отсчета и система координат? Вообще говоря, никак. Выбор базиса касательного пространства — системы отсчета — и выбор системы координат сами по себе не зависят друг от друга. Но эту зависимость можно установить, что называется, руками, если потребовать, чтобы система отсчета в точке $x$ была голономной $\{t_\mu=\partial_\mu\},$ и эта голономность поддерживалась бы при преобразовании системы координат:

$$x^\mu\to x^{\mu'},\quad\partial_\mu\to\partial_{\mu'}=\sum_\nu\dfrac{\partial x^\nu}{\partial x^{\mu'}}\partial_nu.\eqno(2.1)$$

Не только локальную систему отсчета можно задать, исходя из данной системы координат, но и систему координат в окрестности точки можно строить, исходя из заданной в ней локальной системы отсчета. Это-так называемые нормальные координаты, которые мы опишем в разделе 2.1.



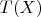
Совокупность всех касательных пространств к многообразию образует касательное расслоение $T(X)$ над $X.$ Чтобы не усложнять изложение, мы не будем давать здесь общего и строгого определения расслоения [47, 53, 60]. Наглядно можно представить себе касательное расслоение как про-, странство $X$ с приклеенными к нему в каждой его точке касательными пространствами $T_x$ (рис. 11). Касательное пространство $T_x$ называется слоем расслоения над точкой $x,$ а само многообразие $X$ — базой расслоения. Определяются еще также следующие конструкции:
сечения расслоения, которые представляют собой дифференцируемые отображения (поднятия) $X$ в $T (X),$ сопоставляющие точке $x$ вектора касательного пространства $T_x$ над $x$; сечения касательного расслоения $\tau(x)$ — это векторные поля на $X$;
атлас расслоения $\Psi =\{(U _\iota,\psi_\iota)\},$ который для каждой точки $x$ из области $U_\iota$ определяет изоморфизм $\psi_\iota(x)$ слоя $T_x$ на стандартное векторное пространство $R^n,$ называемое типичным слоем расслоения.
Такое отображение в общем случае не может быть задано на всем $X,$ и его приходится покрывать областями $U _\iota,$ как для задания системы координат. Если же атлас $\Psi$ может быть выбран состоящим из одной карты $(U =X,\psi),$ расслоение считается тривиальным. Тривиальность или нетривиальность касательного расслоения является топологической характеристикой многообразия. Например, двумерная сфера имеет нетривиальное касательное расслоение, а тор — тривиальное.
Задание атласа касательного расслоения можно рассматривать как задание глобальной системы отсчета, понимаемой как некоторая совокупность локальных систем отсчета, восстановленных в каждой точке многообразия $X.$ Действительно, атласом $\Psi=\{(U_\iota,\psi_\iota)\}$ в каждой точке $x$ из $U_\iota$ определяется базис $\{t_\mu(x)\}_\iota=\{\psi_\iota^{-1}(x)t_\mu\}$ касательного пространства $T _\kappa,$ где $\{ t_\mu\}$ — фиксированный базис типичного слоя $R^n.$ Поле реперов $\{ t(x)\}_\iota$ непрерывно на $U _\iota,$ а на пересечениях $U _\iota\cap U_\kappa$ реперы $\{ t(x)\}_\iota$ и $\{ t(x)\}_\kappa$ связаны функциями перехода $\{ t(x)\}_\iota=(\psi_\iota^{-1}\psi_\kappa)\{t(x)\}_\kappa.$



Если многообразие имеет тривиальное касательное расслоение, то непрерывное поле реперов $\{ t(x)\}$ можно задать на всем $X,$ но в общем случае это не так. Например, его легко построить на торе (рис. 12), но никак не удастся это сделать на сфере.
Как и локальная система отсчета, глобальная система отсчета — атлас $\Psi$ касательного расслоения $T (X)$ — не коррелирует с выбором системы координат — атласа $\Psi_X$ многообразия $X,$ если не требовать специально, чтобы атлас $\Psi$ был голономным, т. е. таким, что определяемые им в каждой точке локальные системы отсчета являются голономными $\{t_\mu(x)=\partial_\mu\}.$ Это важно подчеркнуть, поскольку различие между системами отсчета и системами координат часто игнорируют.
В этой главе, посвященной стандартной ОТО, мы будем рассматривать только голономиые системы отсчета. Поэтому, допуская вольность, вместо слов «преобразования системы отсчета» мы будем порой говорить «преобразования системы координат», подразумевая, что они влекут за собой голономиые преобразования системы отсчета (2.1).

[epros]

Munin в сообщении #512204 писал(а):

Я уже удивился. Вот, значит, до чего может довести введение собственной нестандартной терминологии. Пишете "неинерциальная", а подразумеваете "несинхронизированная"... И это изобретение птичьего языка у вас совместное с zbl и В. Войтик-ом.

Итак, вместо ответов по существу (я же просил посчитать пространственную метрику, чтобы Вы могли убедиться, что линейка нигде не деформировалась, хотя каждая её точка разгонялась с бесконечным ускорением) опять троллинг...

Моя терминология - стандартная, а Вы - не эталон стандартности, как бы ни пытались на это претендовать. Описанная СО неинерциальная в первую очередь потому, что она связана со стержнем, скорость движения которого изменяется. К тому же понятие ИСО автоматически подразумевает синхронность, так что несинхронность автоматически означает, что речь о неинерциальной СО. Разумеется, для этого стержня построить синхронно-сопутствующие координаты невозможно. Но это и не нужно. Для того, чтобы судить о дефомируемости/недеформируемости достаточно иметь просто сопутствующие координаты. Повторяю: их всегда можно построить. У Вас есть что возразить? Я Вам привёл пример, когда сопутствующие координаты строятся для объекта, испытывающего бесконечные ускорения. Что Вам ещё не хватает?

-- Ср дек 07, 2011 10:26:10 --

Утундрий в сообщении #512268 писал(а):

Коротко говоря, СО это совокупности мировых линий

А я бы ещё добавил понятие одновременности (хотя знаю, что Вы против этого возражаете). Иногда всё же хочется различать "до" и "после". Например, в приведённом Выше примере мгновенно разгоняющегося стержня расстояния не зависят от того, как мы проведём гиперповерхности $t = \operatorname{const}$, однако от этого зависят ответы на некоторые другие вопросы. Скажем, ответ на вопрос: "Что раньше разогналось - начало или конец стержня"?

[Munin]

epros в сообщении #512358 писал(а):

Моя терминология - стандартная

Я уже предлагал способ, которым вы можете это продемонстрировать. Ждём-с.

[epros]

(Оффтоп)

Munin в сообщении #512487 писал(а):

Я уже предлагал способ, которым вы можете это продемонстрировать. Ждём-с.

Извините за резкость, но кормить тролля не хочу.

[Munin]

При том, что я стандартность своей терминологии продемонстрировал.

На том и закончим.