4. Let {

} be a sequence of real numbers such that

and

for all
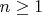
. Show that {

} is convergent and find its limit.
Вот мне сразу в голову, как такое вижу, приходят производящие функции. Ну и вправду, обозначая

производящую функцию

, имеем

, откуда легко находим, что надо.
Кстати, да, это задача о письмах и конвертах. И приведенное рекуррентное равенство имеет очень простую вероятностную интепретацию:
(интепретация)
В левой части -- сумма по

вероятностей того, что первые

писем попадут к адресатам, а остальные не попадут.
Надо будет взять на заметку и добавить такое хитроумное решение задачи про письма и конверты в свой учебник
 -- Пт июл 15, 2011 09:40:28 --
-- Пт июл 15, 2011 09:40:28 --3. Let {

} be a sequence of real numbers such that

. Let

be a continuous function such that

. Show that

Если слово "непрерывная" выбросить, нормальная задача получится. А так, как верно заметил
ewert, детская.
-- Пт июл 15, 2011 09:45:47 --1. Let V be an n-dimensional vector space over

where n is odd number. Let S and T be linear transformations on V such that
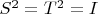
.
Prove there is a one dimensional subspace of V invariant under both S and T.
Принцип Дирихле. У каждого из операторов есть подпространство, чуть более чем половинной размерности, состоящее из собственных векторов.
-- Пт июл 15, 2011 10:05:33 --2.Let {

} be a set of real

matrices which forms a group under matrix multiplication. If
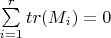
prove
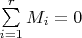
Придумал довольно запутанное доказательство. Подозреваю, что с дыркой, так как у меня получилось, что группа может быть только циклической.
-- Пт июл 15, 2011 10:10:53 --4. Let V be a finite dimensional vector space over C and
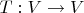
be a linear transformation. Prove that T is diagonalizable if and only if for any
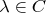
,
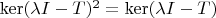
.
Если
такое надо доказывать, то
чем можно пользоваться?
(Оффтоп)
Хотя вот когда я в аналогичном мероприятии участвовал, там была задача в духе "напишите все, что знаете про разделенные разности", это не шутка.
-- Пт июл 15, 2011 10:25:05 --2.Let G be a finite group and
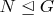
be a normal subgroup of G of order p, where p is a prime number. If p is the least divisor of the order of G prove
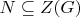
.
Элементы

действуют сопряжением на ненулевых элементах

, коих число

. Очевидно, там не может быть орбит длины больше единицы.
(Оффтоп)
Есть два решения еще короче. Первое -- "куда ей деваться", второе -- "так как наименьший делитель порядка

-- единица, то

" (единицу в Иране вполне могут называть простым числом).
Ну ладно, хватит. Надеюсь, на бронзу я уже нарешал
