2.
Algebra1.Let
be any ring such that
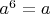
for all
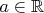
. Show that
is a commutative ring.
2.Let G be a finite group and
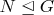
be a normal subgroup of G of order p, where p is a prime number. If p is the least divisor of the order of G prove
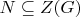
.
3.Let D be an infinite integrals domain. If the number of maximal ideals of D is finite prove that D contains an infinite number of units.
4. Let G be a group and
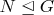
. If
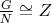
prove there is a subgroup A of G such that
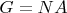
and
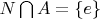
.
3.
Linear Algebra1. Let V be an n-dimensional vector space over

where n is odd number. Let S and T be linear transformations on V such that
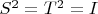
.
Prove there is a one dimensional subspace of V invariant under both S and T.
2.Let {

} be a set of real
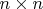
matrices which forms a group under matrix multiplication. If
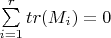
prove
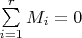
3.Let
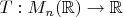
be a linear functional and C be the matrix whose
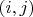
-entry is
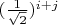
. If
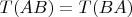
, for every
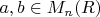
and
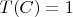
, then compute

.
4. Let V be a finite dimensional vector space over C and

be a linear transformation. Prove that T is diagonalizable if and only if for any
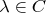
,
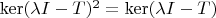
.