Доказать что нельзя определить разность через объединение и пересечение.
Докво:
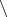
-несимметрическая ф-я

- симметрическая ф-я

-симметрическая ф-я
Так как суперпозиция симм. ф-й также симметрическая ф-я, то ч.т.д
Правильно?
Доказать, что нельзя определить

через
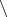
и

.
Док-во:
для док-ва достаточно рассмотреть ситуацию, когда определение невозможно.
-- Ср июн 22, 2011 11:37:01 --Пусть

. Тогда
множество

содержит все элементы множества B, а
ни одно из множеств

-пустое

- A
не содержит всех элементов B.
Ни одна их композиция, очевидно не может содержать всех элементов B(так как в ней учавствуют только пустое и A).
Правильно?