Дочитал. Мне не понятно, почему всюду мерещится Каталан? Как какой пустяк, так сразу Каталан.
Я вообще склонен к видениям

Когда я слышу, что среди чисел вида
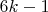
бесконечно много простых, мне мерещится теорема Дирихле о простых числах в арифметической прогрессии.
Когда я слышу, что уравнение

неразрешимо в натуральных числах, что мерится ВТФ...
При этом я вполне отдаю себе отчет в том, что вышеприведенные частные случаи могут быть рассмотрены без доказательства соответствующих теорем в общем виде. Но вот мерещится... и все.
[quote]И зачем людей пугать ...[quote]И такая слабость тоже имеется.
PS: Хотя все же не мерещится, а вспоминается. Мерещится, чудится, мнится то, чего, на самом деле, нет.