У любого средства должна быть достаточно сильная нагрузка, чтобы оно использовалось в полной мере. Когда шрифтом выделяют векторы - это большая нагрузка, потому что векторы могут быть обозначены любыми буквами, векторные выражения могут быть плотным нагромождением букв, и без шрифтов там будет трудно разобраться, а шрифты легко выполняют огромную задачу. Когда шрифтом выделяют многобуквенные обозначения (любые! от синуса до названий категорий до химических элементов), это тоже большая нагрузка.
По сравнению с этим - если выделять "шрифтом для

" только

это нагрузка крайне небольшая.

и так достаточно выделена тем, что это знакомая нам буква латинского алфавита, и мы помним, какое спецзначение за ней закреплено (точно так же, как помним
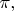


и другие буквы, в зависимости от предметной области). Вводить ещё и шрифт - это избыточность средств при очень небольшой нагрузке. Читатели не обратят внимание на лишнее средство, или даже сочтут его мешающим. Бывают люди, стремящиеся к "украшательствам", но их системы обычно не выживают, в жизни к системе обозначений противоположные требования, и очень жёсткие. Уж на что казалась красивой и эффективной идея использовать фрактуру для обозначения объектов ещё одной природы, например, тензоров - она оказалась избыточной, и вместе с фрактурой практически забыта. В тензорных и вообще индексных обозначениях давно забыли значок суммы. И т. п., примеров много.