Для определения наличия каких-либо групп вычетов в ПСВ
критерий существования групп

необходимо проверять только при


где

-число вычетов группы, сравнимых по модулю

,
не считая вычета, с которым идет сравнеие.
Формулу

c двойной зависимостью от
р непрактична.
Ее надо привести в более удобную форму.
Если мы определим, что при некоторых
р разность

то их надо вынести за знак
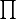
в виде коэффициента


, где

для всех
р, у которых

Если взять натуральную группу вычетов, то для определения критерия

гораздо проще иметь дело с приведенной группой, которая образуется из натуральной
вычитанием первого вычета из всех вычетов группы.
н.п. (11,13,17,19)=(0,2,6,8), здесь сразу видно:

.
Кстати, в приведенном ранее примере для функции

указана группа (4,2,4).
Это не так: (13,17,19,23)=(0,4,6,10), здесь


Следовательно, коэффициент при функции

для указанных групп
