Вас наверное смущает на рис 2 второй вариант? Тут я утрированно изобразил наверное, собственно вариант Первый это есть проекция второго варианта на горизонт...Погуглил и нашел вот такое вот решение...
Пример 2. Найти площадь фигуры, лежащей вне круга

и ограниченной кривой

.

Р е ш е н и е. Так как функция

имеет период

, то при изменении

от

до

радиус-вектор описывает три равных лепестка кривой. При этом допустимыми для

являются те значения, при которых

, откуда


Следовательно, один из лепестков описывается при изменении

от

до

. Остальные два лепестка получаются при изменении
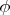
от

до

и от

до

соответственно (рис. 3.2). Вырезая из лепестков части, принадлежащие кругу

, мы получим фигуру, площадь которой нужно определить. Ясно, что искомая площадь равна утроенной площади

Найдем полярные координаты точек пересечения М и N. Для этого решим уравнение

т.е.

. Между

и

находятся только корни

и

.

. Таким образом, точке N соответствует полярный угол

, точке М — угол

.Далее из рисунка заключаем, что


Попробую нарисовать, у меня не абстрактная задача, даны конкретные радиусы окружности и такая синусойда... единственно пробовал по этому найденному примеру решать свою задачу по нахождению шага разбиения, но получается ошибка, у меня радиус в метрах и угол в град (или радианах) и в результате при интегрированнии получается ошибка...