(не понимаю по какому принципу оно возводиться в степень) и порядок

равен 5 и что тут будет единицей

или

,вообщем совсем запутался...
Единицей будет

— тождественная перестановка, которая ничего не переставляет.
Перестановки возводятся в степень по определению степени — умножаются на себя:

. Смотрим, во что переходит каждый элемент множества

: 1 в 2, а потом в 3; 2 в 3, а потом в 5; 3 в 5, а потом в 6; 4 в 4, а потом в 4; 5 в 6, а потом в 1; 6 в 1, а потом в 2. Получаем цикл
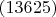
.