Bulinator писал(а):
На указанных Вами страницах только преобразование в.ф..
Опять же, чтобы представить Ваш оператор Гамильтона в базисе

а что вы ожидали увидеть ? вы спросили о там как выглядид оператор в моментном представлении, там ответ.
5 слайд, формула обведена

осталось вспомнить что

и вперед, что вас так удивляет??????
вам не приходилось решать уравнения используя преоброзования Фурье ?
электродимамика по швам трещит, везде этот способ, чем КМ хуже

да

для волновой функции и для Гауссова импульса разные.
на самом деле там надо писать

я уже писал что

и

не коммутируют, но это вылевается лишь в разность фаз.
для

Такой проблемы нет вообще, давайте для него решать в

представлении
Вопрос ведь совсем другой!
почему исчезает время для

Как решить подругому чтобы было все в порядке ?
Bulinator писал(а):
Соответственно, уравнение Шредингера всегда второго порядка. Потому и получали неправильное решение.
Это не так, в координатном представлении оно второго порядка. (Посмотрите любой любой учебник, или Шанкара с149-150.)
Какое решение правельное ???
-- Ср дек 29, 2010 02:55:22 --П.С.
Меня вполне устроит решение с чистого листа,
можно решать в
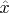
представлении, вопрос только как ???