Даны две случайные величины X и Y, имеющие одинаковые дисперсии, но первая распределена нормально, а вторая равномерно. определить соотношение между их средними отклонениями
вот мой ход решения
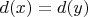
для нормального распределения:
E=корень из2*корень из D(x)*P
где p=0,4769
d-дисперсия
Е-среднее отклонение
для равномерного:
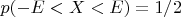
подскажите формулу для среднего отклонения у равномерного распределения.