Этот предел равен бесконечности. Доказать не смогу, но попробую объяснить, почему. Во-первых, я в Maple посчитал значения для

. Растет как экспонента или быстрее, но сильно дергается при этом (при

логарифм это дроби чуть больше 20).
Во-вторых. Я заменю знаменатель суммы из числителя на

. У меня отношение

не превышает 48 для

и более чем в половине случаев равно 1. А знаменатель суммы я проанализировать пока не могу.
Теперь покажем, что

. Пусть

- простое. Если

, то

. Если

и

и

, то в числе

содержится множителей

больше чем в

на

. Поэтому

делится как минимум на

Обозначим

(

) и тогда

делится как минимум на

Теперь вспоминаем, что

, откуда

и

и тогда

растет не медленее, чем
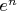
, а тогда

P.S. А почему проверка иррациональности?