Математическая логика

[sasha198407]

Здравствуйте господа. Я сам заочник и поэтому приходится грысть гранит науки самостоятельно. В универе дали учебный материал, только он такое ощущение, что для академиков( нихрена не понятно). Вобщем сижу уже 2 недели над ниже приведёнными задачами и ничего не получается. Если кто знает, обьясните пожалуйста. Есть две задачи.
Задача1
Доказать выводимость формул в исчислении высказываний методом резолюций.
A $\to$ B $\mapsto$(C $\to$ A) $\to$ (C $\to$ B)
Задача2
Записать в алфавите {a0,|,*} программу машины Тьюринга для вычисления заданной функции.
f(n)=n+4

Зарание огромное спасибо.

[Maslov]

sasha198407 в сообщении #269115 писал(а):

Вобщем сижу уже 2 недели над ниже приведёнными задачами и ничего не получается.

А какие-нибудь результаты двухнедельного сидения представить можете?
(Тут на форуме очень строгие правила: пока Вы собственные попытки решения не продемонстрируете, Вам и помогать-то нельзя).

-- Вт дек 08, 2009 18:10:47 --

И почитайте правила набора формул (http://dxdy.ru/topic183.html), а то Ваше обозначение "|-->" довольно загадочно.

[sasha198407]

Покапавшись в интернете и найдя похожую задачу. Я задачу 1 решил.
A $\to$ B $\mapsto$(C $\to$ A) $\to$ (C $\to$ B)

Что бы доказать "если P, то Q", достаточно показать, "если не P, то не Q". Пусть (C $\to$ A) $\to$ (C $\to$ B)= 0 . Докажем, что в этом случае A $\to$ B = 0.
(C $\to$ A) $\to$ (C $\to$ B)= 0
(C $\to$ A) = 1, (C $\to$ B)= 0
С=1 и А=1, С=1 и В=0
С=1,А=1,В=0
В этом случае A $\to$ B =1$\to$ 0=0

Но я так понимаю метод резолюций подразумевает применение формулы
P $\to$ Q $\xymatrix{\ar@{<->}[rrr]&&&}$ не Q v P
Так чёрт возьми в какое место мне впихнуть эту формулу.


По машине Тьюринга понятно как она работает, но не понятно, как производить сложение. Вот пример

//// /$a_{0} $||| || $a_{1} $ ||||| $a_{2} $
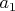
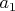
$q_{1} $||$a_{0} $,R,$q_{1} $||$a_{1} $,R,$q_{1} $||$a_{2} $,R,$q_{1} $
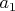
говорит нам, что надо записывать значения $a_{0} $,$a_{1} $,$a_{2} $ и сдвигаться в право, оставаясь в состоянии $q_{1} $
Но я не возьму в толк, как складывать.

[AD]

Maslov в сообщении #269146 писал(а):

И почитайте правила набора формул

Правила есть правила.

Пожалуйста, исправьте написание формул в соответствии с Правилами.
Используйте кнопку для редактирования своего сообщения.

Тема перемещена из "Помогите решить (М)" в карантин. В теме Что такое карантин, и что нужно делать, чтобы там оказаться также описано, как исправлять ситуацию.