Объяснение отрицательного результата опыта Майкельсона

[Yakov-Chin]

Дело в том, что в нашем случае стрельба фотонами ведется в перпендикулярном направлении к движению. Если они воспринимают скорость источника в перпендикулярном направлении, то почему они не должны воспринимать скорость источника по направлению?

[Galina]

EEater в сообщении #260308 писал(а):

Я не Vallav, но охотно объясню. Все дело в относительности одновременности. Из-за нее - в системе отсчета поезда Москва и Ленинград живут в несколько разном времени. Ленинград уже забежал в будущее, и потому поторопился приблизиться. А Москва запоздала в прошлом, поэтому не спешит удалиться. Вот расстояние и сократилось.
Проверьте одновременно часы в Москве и Ленинграде, и Вы убедитесь.
Возьмитесь за изучение физики, порешайте задачи, и все эти вещи Вам будут абсолютно понятны.

Ой, какие интересные объяснения! От того, что релятивист едет в Ленинград, Ленинград забегает в будущее! А Москва по вине релятивиста запоздала в прошлом! Вот это объяснения!

А теперь объясните мне, каким именно образом "забегание в будущее" Ленинграда и "отставание в прошлом" Москвы могут сократить расстояние между Ленинградом и Москвой? Что-то связи не улавливаю?

[EEater]

Yakov-Chin в сообщении #260437 писал(а):

Дело в том, что в нашем случае стрельба фотонами ведется в перпендикулярном направлении к движению. Если они воспринимают скорость источника в перпендикулярном направлении, то почему они не должны воспринимать скорость источника по направлению?

Чувствую, без формул не обойтись.
Итак, лазер стреляет по мишени. Расстояние $d$, скорость света $c$, время в пути $t=d/c$.
Теперь перейдем в другую ИСО - в такую, в которой связка "лазер-мишень" движется со скоростью $v$, причем отрезок, их соединяющий, направлен поперек линии движения.
За время $t=d/c$ (по часам связки) свет достигает линии мишени. Но по часам лабораторной ИСО прошло времени больше: $t_1 = \frac {t}{\sqrt{1-v^2 /c^2}}$. То есть составляющая скорости света, направленная перпендикулярно, равна $d/t_1 = c \sqrt{1-v^2 /c^2}$.
Составляющая скорости света вдоль движения, по теореме Пифагора (причем гипотенуза равна $c$): $\sqrt{c^2 - c^2 (1-v^2 / c^2)}=v$. Таким образом, луч находится все время на поперечной линии мишени, и потому попадает в нее.

[Galina]

peregoudov в сообщении #260321 писал(а):

Сначала усовершенствуем картинку, обозначив буквами необозначенные ключевые точки.

Спасибо! Очень мило с вашей стороны.

peregoudov в сообщении #260321 писал(а):

Если бы свет падающей волны одновременно достигал точек C и Е, можно было бы утверждать, что он одновременно достигает точек В и D. Однако это не так. Свет достигает точки Е позже, чем точки С.

С чего вы это взяли? Фронт №1 достигает точки С в тот же самый момент времени, когда фронт №2 достигает достигает точки Е. Оба события происходят совершенно одновременно. Мало того, картинка как раз и нарисована в момент этого знаменательного события. Как раз в обозначенный момент фронт №1 достиг С, а фронт №2 достиг Е. Далее события развиваются так - фронт №1 продвигается в точку В. А из точки Е растет вторичный фронт до радиуса ЕD. Расстояния ВС=ЕD. Теперь проводим из точки В касательную к окружности - вуаля! Правильный фронт готов!

Но имейте в виду, что наши с вами "доказательства" - это филькина грамота, до тех пор, пока они не будут удостоверены экспериментально. Мое утверждение о равенстве углов падения и отражения подтверждено тысячами экспериментов.

Ваше же голословнейшее утверждение о неравенстве углов падения и отражения не подтверждены НИЧЕМ, ни единым экспериментиком. Это очередной постулатишко , в который верующим приказано верить не думая.

-- Вт ноя 10, 2009 12:42:31 --

peregoudov в сообщении #260321 писал(а):

Эксперимент с лазером в школьном коридоре повеселил. А вот petrovich1964 с Сайтека проводил аналогичный эксперимент и утверждает, что смещения луча нету.

Подключайтесь, тоже проводите этот эксперимент. Сами лично удостоверитесь, что ТО - лженаука.

[EEater]

Galina в сообщении #260445 писал(а):

Ой, какие интересные объяснения! От того, что релятивист едет в Ленинград, Ленинград забегает в будущее! А Москва по вине релятивиста запоздала в прошлом! Вот это объяснения!

Если категорически не признавать, что время относительно и зависит от системы отсчета, то такие объяснения, естественно, ничего не объяснят, Вы правы.

Galina в сообщении #260445 писал(а):

А теперь объясните мне, каким именно образом "забегание в будущее" Ленинграда и "отставание в прошлом" Москвы могут сократить расстояние между Ленинградом и Москвой? Что-то связи не улавливаю?

Странно, что не улавливаете. Движущийся навстречу нам Ленинград находится (в нашей ИСО) там, где должен быть в 10:00 по своим часам. А у удаляющейся Москвы часы показывают 9:59. Она находится там, где ей и положено быть в это время: ближе к Ленинграду, чем ей следовало, на скорость поезда, умноженную на 1 минуту.
Вся проблема в том, что мы засекаем положение Москвы и Ленинграда в одно время по часам, движущимся вместе с поездом, но они, увы, идут не так, как вокзальные часы в городах.

[Galina]

Vallav в сообщении #260399 писал(а):

Спасибо за разъяснение, но Вы забыли ответить на
главное -
То есть, эксперимент у них ставился так - начинали поворачивать установку.
Луч смещался, что вызывало сдвиг полос. Они подкручивая зеркало возвращали полосы назад, в исходное состояние.
И результат эксперимента - подкруткой зеркала можно добится того,
чтобы полосы при повороте не смещались.
Вам такая постановка эксперимента не кажется несколько странной?

Извините, пожалуйста, что не ответила раньше, была очень занята, да и сейчас пишу на работе, украдкой.

Мне вообще весь эксперимент кажется странным.

Давайте подождем с обсуждением, как именно проводился эксперимент до того, как получим результаты экспериментов с лазерной указкой. Давайте все лично удостоверимся, что смещение луча происходит (или не происходит), а уже потом будем думать, что делал Майкельсон. Без знания того, что происходит с лучом при движении Земли мы не может продвигаться дальше.

Поэтому, будьте другом, купите тоже эту лазерную указку и тоже проведите эксперимент.

[Galina]

Vallav в сообщении #260399 писал(а):

Спасибо за разъяснение, но Вы забыли ответить на
главное -
То есть, эксперимент у них ставился так - начинали поворачивать установку.
Луч смещался, что вызывало сдвиг полос. Они подкручивая зеркало возвращали полосы назад, в исходное состояние.
И результат эксперимента - подкруткой зеркала можно добится того,
чтобы полосы при повороте не смещались.
Вам такая постановка эксперимента не кажется несколько странной?

Извините, пожалуйста, что не ответила раньше, была очень занята, да и сейчас пишу на работе, украдкой.

Мне вообще весь эксперимент кажется странным.

Давайте подождем с обсуждением, как именно проводился эксперимент до того, как получим результаты экспериментов с лазерной указкой. Давайте все лично удостоверимся, что смещение луча происходит (или не происходит), а уже потом будем думать, что делал Майкельсон. Без знания того, что происходит с лучом при движении Земли мы не может продвигаться дальше.

Поэтому, будьте другом, купите тоже эту лазерную указку и тоже проведите эксперимент.

-- Вт ноя 10, 2009 12:51:22 --

EEater в сообщении #260451 писал(а):

Вся проблема в том, что мы засекаем положение Москвы и Ленинграда в одно время по часам, движущимся вместе с поездом, но они, увы, идут не так, как вокзальные часы в городах.

Мы засекаем положение Москвы и Ленинграда с помощью метра и линейки, а не с помощью часов.

Как показания часов могут изменить расстояние между Москвой и Ленинградом?

-- Вт ноя 10, 2009 12:53:56 --

EEater в сообщении #260451 писал(а):

Странно, что не улавливаете. Движущийся навстречу нам Ленинград находится (в нашей ИСО) там, где должен быть в 10:00 по своим часам. А у удаляющейся Москвы часы показывают 9:59. Она находится там, где ей и положено быть в это время: ближе к Ленинграду, чем ей следовало, на скорость поезда, умноженную на 1 минуту.

Значит Москва и Ленинград наблюдают за часами, и в соответствии с показаниями часов релятивиста перемещаются в пространстве?

А как они перемещаются? С помощью моторчика? Или движением мысли релятивиста?

[EEater]

Galina в сообщении #260454 писал(а):

Значит Москва и Ленинград наблюдают за часами, и в соответствии с показаниями часов релятивиста перемещаются в пространстве?
А как они перемещаются? С помощью моторчика? Или движением мысли релятивиста?

Сарказм не работает. Точнее, работает против того, кто не знает, что движение относительно, а также бывает перемещение без моторчика (темы, кажется, 6-го класса школы).
Не стоит острить в мой адрес, не я это все открыл (а хотел бы!). А физике от Ваших острот ни холодно, ни жарко.
Москва и Ленинград перемещаются в строгом соответствии со своими часами, называется - собственное время.

[Yakov-Chin]

Цитата:

Чувствую, без формул не обойтись.
Итак, лазер стреляет по мишени...... Таким образом, луч находится все время на поперечной линии мишени, и потому попадает в нее.

Это все математическая казуистика. К любой теории можно использовать соответствующую математику, но соответствует ли это физическому смыслу? Я задаю вопрос о физическом смысле постулата о независимости скорости света от скорости источника. Повторюсь, хотя это бессмыслено, если фотоны воспринимают скорость источника в перпендикулярном направлении, то почему они не должны воспринимать скорость источника по направлению своего движения? В перпендикулярном направлении скорость прибавляется, т.е. с ними обращаются как с любым другим веществом, а в направлении движения фотона скорость фотона не меняется и равна с.

-- Вт ноя 10, 2009 18:56:53 --

Кстати, о Москве и Ленинграде. Существует парадокс. Самолет из Москвы до Ленинграда долетает за 1 час 20 минут, а обратно всего лишь за восемдесят минут. Но СТО и ветер здесь ни причем.

[arseniiv]

Yakov-Chin в сообщении #260468 писал(а):

Существует парадокс. Самолет из Москвы до Ленинграда долетает за 1 час 20 минут, а обратно всего лишь за восемдесят минут.

Да ну, этот "парадокс" все уже знают, он неинтересный совсем.

Yakov-Chin в сообщении #260468 писал(а):

К любой теории можно использовать соответствующую математику, но соответствует ли это физическому смыслу?

Не к любой теории. К логически противоречивой не получится, например.

Yakov-Chin в сообщении #260468 писал(а):

Повторюсь, хотя это бессмыслено, если фотоны воспринимают скорость источника в перпендикулярном направлении, то почему они не должны воспринимать скорость источника по направлению своего движения? В перпендикулярном направлении скорость прибавляется, т.е. с ними обращаются как с любым другим веществом, а в направлении движения фотона скорость фотона не меняется и равна с.

1. Нарисуйте прямоугольный треугольник. Гипотенуза имеет длину c, один из катетов - скорость передатчика. Другой - проекция скорости фотона на перпендикулярную движению передатчика ось.
2. Делить материю на "вещество" и "энергию" бессмысленно. Энергия - это свойство проявляющей себя в нашем мире материи. (А то вы говорите о фотонах, что они не вещество.)
3. Вы едете по катку с какой-то скоростью. Запустите по льду шайбу перпендикулярно вашей траектории и вы увидите, что шайба движется "как надо", а другие увидят, что она движется не перпендикулярно траектории, а под углом. Чем хуже фотоны?

[EEater]

Yakov-Chin в сообщении #260468 писал(а):

Это все математическая казуистика.

???
А я думал - честная математика...

Yakov-Chin в сообщении #260468 писал(а):

В перпендикулярном направлении скорость прибавляется, т.е. с ними обращаются как с любым другим веществом, а в направлении движения фотона скорость фотона не меняется и равна с.

Если я правильно Вас понял... Ну просто свойство у света такое. В направлении распространения его скорость возрасти не может - она предельна, так устроена природа. Но может измениться направление - вот оно и меняется при переходе в другую ИСО.
Между прочим, физически это изменение объяснимо, если вы рассмотрите апертуру лазера. При смене ИСО - фазовый фронт на апертуре наклоняется из-за того, что ее точки перестали быть одновременными! Вот луч и идет вкось. Так работают фазированные антенные решетки.

[peregoudov]

Galina в сообщении #260450 писал(а):

Цитата:

Если бы свет падающей волны одновременно достигал точек C и Е, можно было бы утверждать, что он одновременно достигает точек В и D. Однако это не так. Свет достигает точки Е позже, чем точки С.

С чего вы это взяли? Фронт №1 достигает точки С в тот же самый момент времени, когда фронт №2 достигает достигает точки Е. Оба события происходят совершенно одновременно.

Ну что же, идиотизм все ярче и ярче.

Одновременно с точкой С свет (свет, а не фронт) достигает точки А. Именно поэтому С и А лежат на одном фронте. Точка Е лежит на другом фронте. Ее свет достигает позже.

При вашем идиотском подходе зачем вообще морочиться с отражением? Просто берем две точки на двух разных фронтах, например, те же точки С и Е. И проводим через них новый "фронт". Ведь

Цитата:

Фронт №1 достигает точки С в тот же самый момент времени, когда фронт №2 достигает достигает точки Е. Оба события происходят совершенно одновременно.

Ну и хрен с ним, что построенный "фронт" пересекает оба исходных фронта (фронт 1 и фронт 2)! И возвращаемся к моей картинке


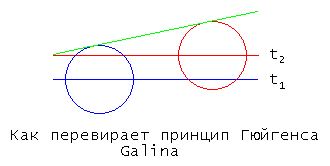
Понятно, что при таком идиотском подходе

Galina в сообщении #260450 писал(а):

"доказательства" - это филькина грамота

"Доказательства" от Galina. О чем я и говорю уже давно.

И еще один сюжет, чтобы покончить с Саньяком и всякими идиотскими высказываниями, что этот эксперимент доказывает какое-то там "сложение". Начнем с рисунка.


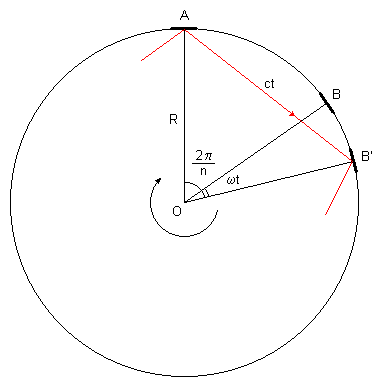
Пусть кольцевой интерферометр состоит из "n" равномерно распределенных по окружности радиуса R зеркал и вращается по часовой стрелке с угловой скоростью $\omega$. На рисунке два соседних зеркала А и В обозначены жирными отрезками. Угол между радиусами, направленными на зеркала, равен $2\pi/n$. Пусть в начальным момент времени луч света, распростаняющийся в интерферометре по часовой стрелке (он показан на рисунке красным), отразился от зеркала А. Вычислим, через какое время t он отразится от зеркала В. Пока луч будет распространяться от А к В, само зеркало В успеет сместиться и примет положение B', за время t интерферометр успеет повернуться на угол $\omega t$. Луч света за это время успеет пройти расстояние ct. Применяя теорему косинусов к треугольнику AB'O, пишем

$$ (ct)^2=2R^2[1-\cos(2\pi/n+\omega t)]. $$

Снова к зеркалу А, сделав круг, луч вернется через время T=tn. Выражая отсюда t и подставляя в уравнение, получим уравнение для T

$$ (cT)^2=2n^2R^2\left[1-\cos\frac{2\pi+\omega T}n\right]. $$

В общем виде это уравнение аналитически решить нельзя, поэтому рассмотрим два частных случая.

1. Бесконечное число зеркал ($n\to\infty$). Используя разложение

$$ \cos x=1-x^2\!/2+\ldots,\quad x\ll1, $$

получаем

$$ (cT)^2=R^2(2\pi+\omega T)^2+\ldots, $$

откуда

$$ cT=\frac{2\pi R}{1-\omega R/c}+\ldots. $$

2. Медленное вращение ($\omega R/c\ll1$). Переписываем уравнение в виде

$$ (cT/R)^2=2n^2\left[1-\cos\frac{2\pi+(\omega R/c)(cT/R)}n\right]. $$

Величина (cT/R) при $\omega=0$ остается конечной, раскладывая косинус по формуле

$$ \cos(a+x)=\cos a-x\sin a+\ldots,\quad x\ll1, $$

находим

$$ (cT/R)^2=2n^2\left[1-\cos\frac{2\pi}n+\frac{\omega T}n\sin\frac{2\pi}n+\ldots\right], $$

откуда

$$ cT=R\left[2n\sin\frac\pi n+\frac{\omega R}cn\sin\frac{2\pi}n\right]+\dots $$

Разумеется, ответы в пунктах 1 и 2 согласованы друг с другом: если в ответе пункта 1 перейти к пределу $\omega R/c\ll1$, а в ответе пункта 2 --- к пределу $n\to\infty$, то получатся одинаковые формулы

$$ cT=2\pi R(1+\omega R/c)+\dots $$

Зная время кругового прохода луча по часовой стрелке, нетрудно написать и время прохода против часовой, для этого надо только изменить знак угловой частоты $\omega$. Поэтому разность времен пробега лучей в случае 1 равна

$$ c\,\Delta T=\frac{2\pi R}{1-\omega R/c}-\frac{2\pi R}{1+\omega R/c}=\frac{4\pi R^2\omega/c}{1-(\omega R/c)^2}, $$

а разность времен пробега в случае 2 равна

$$ c\,\Delta T=R\left[2n\sin\frac\pi n+\frac{\omega R}cn\sin\frac{2\pi}n\right]-{}$$

$${}-R\left[2n\sin\frac\pi n-\frac{\omega R}cn\sin\frac{2\pi}n\right]=\frac{2nR^2\omega}c\sin\frac{2\pi}n. $$

В обоих случаях разность времен пробега (то есть смещение полос) пропорциональна угловой скорости и обращается в нуль, если прибор не крутится.

Никакого "сложения скоростей" (ни "классического", ни "релятивистского") при выводе не использовалось.

[Yakov-Chin]

arseniiv

Цитата:

Вы едете по катку с какой-то скоростью. Запустите по льду шайбу перпендикулярно вашей траектории и вы увидите, что шайба движется "как надо", а другие увидят, что она движется не перпендикулярно траектории, а под углом. Чем хуже фотоны?

И я о том же. Классические представления, но они работают в выборочных направлениях.

[arseniiv]

Не в выборочных! Вы что, не поняли, там практически то же самое! Просто фотон не может изменить модуль скорости, а шайба может. Но операции с векторами скорости там такие же! (Просто, в ТО они подправлены для учёта максимальности c. Фотоны же движутся с c потому, что безмассовы, как и глюоны и гипотетические гравитоны.)

Вы вектора складывали когда-нибудь вообще?

[peregoudov]

Вообще-то отклонение луча при движении источника действительно можно трактовать как "сложение скоростей". Только не классическое, а релятивистское. И, разумеется, не в "выборочных направлениях", а во всех направлениях. Преобразование скорости "u" из нештрихованной ИСО в штрихованную выглядят так

$$ u'_x=\frac{u_x+v}{1+u_xv/c^2},\quad u'_y=\frac{u_y\sqrt{1-v^2/c^2}}{1+u_xv/c^2}. $$

(ИСО движутся относительно друг друга со скоростью "v" в направлении оси "x"). Рассмотрим два случая.

1. В нештрихованной ИСО свет вылетает по направлению движения (по оси "x"), $u_x=c$, $u_y=0$. Подставляя в формулы преобразования, получаем

$$ u'_x=c,\quad u'_y=0. $$

2. В нештрихованной ИСО свет вылетает перпендикулярно
направлению движения (по оси "y"), $u_x=0$, $u_y=c$. Подставляя в формулы преобразования, получаем

$$ u'_x=v,\quad u'_y=c\sqrt{1-v^2/c^2}. $$