Вы не сможете определить, является ли мой текст не математическим. Для этого, по крайней мере, нужны математические возражения с Вашей стороны, нахождение у меня ошибок, каких-нибудь явных нелепостей. Ошибок и нелепостей Вы не нашли. Математическими являются даже очень корявые древние тексты, не говоря уже о том, что мой текст существенно более точный, чем древние. Но это лирика. В тексте по ссылкам всё досконально объяснено, причём, там текст такой же, как и здесь, выложенный на форуме.
Отношение эквивалентности между функциями определялось, см.
http://dxdy.ru/topic23150.htmlhttp://dxdy.ru/post232598.html#p232598Определяю ещё раз:

, если для всех достаточно больших

оказывается

.
 эквивалентна
эквивалентна 
, если для всех достаточно больших

оказывается

.
По остальному несколько позже.
-- Вт авг 04, 2009 21:37:24 --Очевидно, что существует функция

такая, что для всех

будет


можно задать и для исходных

и

, полагая

. Ясно, что на интервале сравнения

и

она будет лежать между ними, оставаясь при этом непрерывной.
Функция

не обязательно должна иметь вид

, так как неравенство

должно быть верно для любого

. Так что Вы приводите слишком частный случай. Ещё раз тогда поясняю: Путём замены функций

и

на эквивалентные функции

и

всегда легко добиться, чтобы для каждого конкретного

было выполнено неравенство

. По аксиоме Дедекинда, применённой для фиксированного

, получаем, что для этого

существует число

такое, что оказывается

. Объявляем это

значением функции

в точке

, т.е.

. Есть ньюанс, что

должна быть непрерывной. Требование непрерывности к

легко выполнимо некоторым тривиальным варьированием эквивалентных функций. Это есть доказательство вообще для произвольных функций, удовлетворяющих условиям свойства I. Странно, что Вы застряли на такой простой вещи.
Функцию

строим как "диагональную" функцию для функций

таких, что для всех

выполнено

, когда

эквивалентны

вот тут требуются разъяснения насчет "диагональной" функции.
Разъясняю: Берём произвольную сторого возрастающую последовательность точек
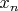
, стремящуюся к 1. В качестве

берём произвольную непрерывную функцию, для котрой оказывается, что

на интервале от
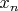
до

. Т.е. функцию "перечёркивающую все остальные", "диагональную". Для такой

по определению оказывается, что

и, следовательно,

. Это подробно пояснено в основном тексте по ссылке.
rishelie писал(а):
Теперь о построении. Вот вам простой пример (проще некуда). множество А содержит функцию

, множество Б содержит функции

. Как вы строите

, большую функции

и меньшую всех функций
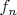
? замечу, что А и Б удовлетворяют условиям Следствия I, ибо все

сравнимы между собой и А меньше Б для всех соответствующих пар функций из А и Б. Сразу скажу, что искомая

существует, причем их можно найти очень много, континуум. Мне интересен ваш мыслительный процесс здесь.
Правильно рассуждаете. Только очень частный случай.
Далее, Вы приводите некие определения, сводимые к ещё более простым функциям. Я могу дать переопределения так, что все теоремы моей работы окажутся теоремами относительно функций, определённых на натуральном ряду и со значениями в этом ряду. Но это не надо. Будет слишком искусственно. Во-первых моё право из эстетических соображений представить теоремы так как Я хочу. Во-вторых, геометрическое выражение аксиом оказывается очень полезным, а его лучше формулировать в рамках непрерывных функций. В третьих. В окончательных доказательствах, касающихся выражения аксиом как теорем теории множетств, требуется применить некоторый приём непрерывного движения линий (и даже не Ваших функций). Так что мой математический подход оправдан полностью.
rishelie писал(а):
...Согласны, что это еще больше упрощает Вашу модель? И в данном случае можно говорить о диагональной последовательности.
Согласен, что можно строить диагональную последовательность в том духе, который я указал. Но замечу, что никакой
моей модели я не строю, нахожусь строго в рамках математического анализа, который, считаем находится в рамках ZFC, например. В частности, все выводы о функциях это выводы не в рамках какой-то моей мифической модели, а выводы математического анализа, не зависящие, например, от принятия или отрицания континуум-гипотезы. Если же Вы знаете какую-то там модель, то не намекайте, а скажите прямо.