Очень лаконично, но куда делись функции распределения с.в.

и

?
Все предыдущие рассуждения и были нужны для того, чтобы вычислить

через

и

.
Скажу Вам по секрету, в течении последующих 25-лет брал немеренное кол-во раз, не помогло. А если-бы задача решалась так элементарно, я бы не потревожил Вас. Извините.
А без этого Вы все равно, скорее всего, задачу не решите ... Хотя не знаю, вот тут
Горьковчанин что-то предложил - другое, но вроде не менее страшное. А какая разница - читать то, что написал я, или читать учебник?
Ну ладно, так уж и быть. Только надо определиться с обозначениями, а то у нас у всех тут они разные. У меня

- плотность,

- распределение,

- характеристическая функция,
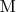
- матожидание.
По определению, характеристической функцией любой случайной величины

называется функция

,

. По формуле матожидания функций от случайных величин получаем

. А если случайная величина

абсолютно непрерывна, то есть имеет плотность, то будет

. В курсе матана такая штука называется преобразованием Фурье функции

.
Если повезёт, а именно, если, скажем, функция

окажется абсолютно интегрируема на

, то будет иметь место обратная формула:

. Скорее всего, это - всё, что нужно знать.
Неужели слабо то же самое в учебнике прочитать?