простите за опечатку-детериминант....
ход решения:



решаем...
получаем:



----------------------------------------
тогда при

:



отсюда:
при

,

,

.
тогда:

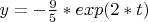

----------------------------------------
При

....решаем аналогично....
----------------------------------------
При

....решаем аналогично.....
----------------------------------------
получаем


....итд....

теперь считаем детерминант,отбросив все константы

из вышенаписанной сис-мы...
он то и полуается равным нулю....