Обсуждение и разбор марафонских задач

[VAL]

(Оффтоп)

Masik в сообщении #916810 писал(а):

VAL в сообщении #914787 писал(а):

Как это у меня бывает, формулировка ММ197 получилась, мягко говоря, невнятным

А Вы в каком школе учили русского языка?

В хорошем.
У меня твердый тройка был. А что?

[Утундрий]

(Оффтоп)

VAL в сообщении #916825 писал(а):

У меня твердый тройка был.

Вах!

[Masik]

(Оффтоп)

VAL в сообщении #916825 писал(а):

У меня твердый тройка был.

Вах!

[VAL]

===========ММ195===============

ММ195 (7 баллов)

Доказать, что для любого натурального числа n, найдется натуральное m, такое что существует не менее n треугольников с целочисленными сторонами и медианой m.

Решение

Приведу решения Дмитрия Пашуткина (наиболее типичное), Константина Хадаева (тоже очень короткое) и Олега Полубасова (с оценками зависимости между n и m).

Вложение:

Комментарий к файлу: Решение Дмитрия Пашуткина
MM195_Pashutkin.pdf [62.73 Кб]
Скачиваний: 496

(Решение Константина Хадаева)

Цитата:

MM195
Рассмотрим прямоугольный пифагоров треугольник со сторонами $2ab, a^2-b^2, a^2+b^2$, медиана равна $(a^2+b^2)/2$. Поэтому достаточно, чтобы $2m$ представлялось в виде суммы квадратов достаточно большим числом способов. Известно, что если $N=2p_1\cdots p_k$, где $p_i\equiv 1\bmod 4$, то количество представлений равно $2^{k-1}$, что можно сделать сколь угодно большим, поскольку простых вида $4t+1$ бесконечно много.

Вложение:

Комментарий к файлу: Решение Олега Полубасова
MM195_Полубасов.pdf [367.64 Кб]
Скачиваний: 487

Обсуждение

Почему эта достаточно простая задача оценена в 7 баллов?
Дело в том, что изначально я планировал указать в формулировке, что треугольники должны быть разносторонними. Но (как со мной это нередко бывает) забыл. Я хотел было уточнить условие, но тут поступило решение Константина Хадаева, которое, с было весьма простым, но не опиралось на равнобедренные треугольники (хотя, по сути, решение Константина, как большинство присланных решений опирается на рассмотрение пифагоровых троек). После этого менять условие не имело смысла.
Любопытно, что большинство участников для получения требуемого результата обошлись не просто пифагоровыми тройками, а тройками, в которых один из катетов - степень двойки.
В решении Антона Никонова по сути рассмотрены случаи $d=2$ и $d=4$ из решения Олега Полубасова.

Последовательность из решения Олега Полубасова безусловно должна попасть в OEIS. Предлагаю Олегу добавить ее туда. В противном случае сделаю это сам.

Награды

За углубленное решение задачи ММ195 Олег Полубасов получает 10 призовых баллов, Антон Никонов - 9 призовых баллов. За правильное решение задачи Константин Хадаев, Виктор Филимоненков, Ариадна, Дмитрий Пашуткин, Анатолий Казмерчук и Сергей Половинкин - получают по 7 призовых баллов.

Эстетическая оценка задачи - 4.5 балла

[Masik]

VAL в сообщении #917608 писал(а):

Последовательность из решения Олега Полубасова безусловно должна попасть в OEIS. Предлагаю Олегу добавить ее туда. В противном случае сделаю это сам.

Без меня. Я зарабатываю свою репутацию другими средствами. Тем более, формулы-то нет.

-- 11.10.2014, 16:28 --

VAL в сообщении #917608 писал(а):

Почему эта достаточно простая задача оценена в 7 баллов?

Не согласен, что задача простая. На мой взгляд, очень даже сложная и интересная. Спасибо! А вот следующая - гораздо проще, а оценивается почему-то больше.

[VAL]

===========ММ196===============

Задача ММ 196 составлена Олегом Полубасовым по мотивам ММ186

ММ196 (9 баллов)

1. Три корабля A, B, и C движутся равномерно и прямолинейно.
2. Когда корабль A находился ближе всего к маяку, расстояние между B и C было 30 миль.
3. Когда корабль B находился ближе всего к маяку, расстояние между A и C было 40 миль.
4. Когда корабль C находился ближе всего к маяку, расстояние между A и B было 14 миль.
5. В 12:00 расстояния от маяка до всех кораблей были одинаковыми.
6. В 13:00 расстояния от маяка до всех кораблей были одинаковыми.
7. В 14:00 расстояния от маяка до всех кораблей были одинаковыми.
8. В 15:00 корабль B пересек маршрут корабля A.
9. В 16:00 корабль A пересек маршрут корабля B.
Найти скорость каждого корабля.
Примечание: Все корабли и маяк - материальные точки.

Решение

Приведу решения Сергея Половинкина, Константина Кнопа и Ариадны.

Вложение:

Комментарий к файлу: Решение Константина Кнопа
mm196-Кноп.doc [19 Кб]
Скачиваний: 489

Вложение:

Комментарий к файлу: Решение Сергея Половинкина
mm196_Polovinkin.pdf [118.44 Кб]
Скачиваний: 492

Вложение:

Комментарий к файлу: Решение Ариадны
196_Ариадна.pdf [602.09 Кб]
Скачиваний: 509

Авторское решение Олега Полубасова приведу в отдельном сообщении.

И, наконец, для любителей ужастиков (слабонервным, детям и женщинам - не смотреть) приведу решение Антона Никонова.

(Решение Антона Никонова)

Цитата:

MM196
Поскольку автору может быть интересно обобщение, переформулирую условие, заменив конкретные значения переменными:

1. Три корабля A, B и C движутся равномерно и прямолинейно.
2. Когда корабль A находился ближе всего к маяку, расстояние между B и C было равно $a$ миль.
3. Когда корабль B находился ближе всего к маяку, расстояние между A и C было равно $b$ миль.
4. Когда корабль C находился ближе всего к маяку, расстояние между A и B было равно $c$ миль.
5. Вначале расстояния от маяка до всех кораблей были одинаковыми и равны $x$.
6. Спустя $q$ часов расстояния от маяка до всех кораблей были одинаковыми и равны $y$.
7. Спустя $s$ часов расстояния от маяка до всех кораблей были одинаковыми и равны $z$.
8. Спустя $m$ часов корабль B пересек маршрут корабля A.
9. Спустя $n$ часов корабль A пересек маршрут корабля B.
Найти скорость каждого корабля.
Примечание: Все корабли и маяк - материальные точки.
------------------------------------------------------------------------------------

Решение


Как и в задаче ММ186, поставил маяк в начало декартовых координат. Как и в задаче ММ186, направление движения одного из кораблей задал произвольно.

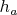
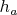
Пусть корабль А движется в этих координатах строго на восток со скоростью $v_a$ на постоянной высоте $h_a$ над горизонтальной осью. Тогда $h_a$ - это и есть минимальное расстояние от корабля A до маяка.

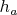
При решении ММ186 мною уже были получены прямые формулы для вычисления $h_a$ и $v_a$:

$h_a = \sqrt{\frac{q^4(x^4 + z^4 - 2x^2z^2) - 2qs(2q^2(x^4 - x^2z^2) - qs(3x^4 - x^2(y^2 +z^2) - y^2z^2) + 2s^2(x^4 - x^2y^2)) + s^4(x^4 + y^4 - 2x^2y^2)}{4q^3s(z^2 - x^2) + 4q^2s^2(2x^2 - y^2 - z^2) - 4qs^3(x^2 - y^2)}}$

$$v_a = \frac{\sqrt{x^2-h_a^2}-\sqrt{y^2-h_a^2}}q$$

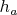
Поскольку, согласно условию, величины $x$, $y$, $z$ для всех 3-х кораблей одинаковы, это неминуемо означает, что и минимальные расстояния всех трёх кораблей $h_a$, $h_b$, $h_c$, а также их скорости $v_a$, $v_b$, $v_c$ одинаковы и в дальнейшем будут обозначаться $h$ и $v$ соответственно. Значит существует и единое время достижения минимума $t_{min}$ для всех кораблей. Очевидно подходящим является время

$$t_{min}=\frac{m+n}2$$

В этот момент корабли образуют треугольник ABC с заданными в условии сторонами. Так как именно в этот момент расстояния от всех кораблей до маяка равны $h$, то они равны радиусу $R$ описанной вокруг треугольника окружности:

$$h = R = \frac{abc}{\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}$$

Итак, величины $t_{min}$ и $h$ известны.


Абсцисса $xprs$ точки пересечения маршрутов может быть найдена двумя способами:

$xprs = 0 + v(n - \frac{m+n}2) = v\frac{n - m}2$

$xprs = xB_{min} - v\cos{u}\frac{n - m}2$

$$v\frac{n - m}2 = xB_{min} - v\cos{u}\frac{n - m}2$$

$$xB_{min} = v\frac{n - m}2(1 + \cos{u})\qquad\text{ (1)}$$

$$xB_{min}^2 = v^2\frac{(n - m)^2}4(1 + \cos{u})^2$$

Ордината $yprs$ точки пересечения маршрутов может быть найдена двумя способами:

$yprs = h$

$yprs = yB_{min} - v\sin{u}\frac{n - m}2$

где $yB_{min} = \sqrt{(h^2 - xB_{min} ^ 2)}\qquad\text{ (2)}$

$$h = \sqrt{(h^2 - xB_{min} ^ 2)} - v\sin{u}\frac{n - m}2$$

$$h^2 - xB_{min} ^ 2 = (h + v\sin{u}\frac{n - m}2)^2$$

$$ -xB_{min} ^ 2 = h^2 + hv\sin{u}(n - m) + v^2\sin^2{u}\frac{(n - m)^2}4 - h^2$$

$$ xB_{min} ^ 2 = -hv\sin{u}(n - m) - v^2\sin^2{u}\frac{(n - m)^2}4$$

$$v^2\frac{(n - m)^2}4(1 + \cos{u})^2 = -hv\sin{u}(n - m) - v^2\sin^2{u}\frac{(n - m)^2}4$$

$$v\frac{(n - m)^2}4(1 + \cos{u})^2 + v\sin^2{u}\frac{(n - m)^2}4 = -h\sin{u}(n - m) $$

$$ v\frac{(n - m)^2}4((1 + \cos{u})^2 + sin^2{u}) = -h\sin{u}(n - m) $$

$$ v\frac{(n - m)}4((1 + \cos{u})^2 + sin^2{u}) = -h\sin{u} $$

$$ v(n - m)(1 + 2\cos{u} + \cos^2{u} + sin^2{u}) = -4h\sin{u} $$

$$ v(n - m)(2 + 2\cos{u}) = -4h\sin{u} $$

Получена формула для искомой скорости кораблей:

$$ v = \frac{-2h\sin{u}}{(n - m)(1+\cos{u})} $$

Другая формула для той же скорости следует из (1):

$$ v = \frac{2xB_{min}}{(n - m)(1+\cos{u})} $$

$$ \frac{2xB_{min}}{(n - m)(1+\cos{u})} = \frac{-2h\sin{u}}{(n - m)(1+\cos{u})} $$

$$ xB_{min} = -h\sin{u} $$

Подставил значение $xB_{min}$ в формулу (2):

$$ yB_{min} = \sqrt{h^2 - (-h\sin{u})^ 2} $$

$$ yB_{min} = h\sqrt{1 - \sin^2{u}} $$

$$ yB_{min} = h\cos{u} $$

В результате решения системы из 3-х уравнений(если нужны подробности, то позже) получил кубическое уравнение, единственным невырожденным решением которого является

$$\cos{u} = 1-\frac{c^2}{2h^2}$$

А искомая скорость всех кораблей равна

$$ v = \frac{2hc}{(n - m)\sqrt{4h^2-c^2}} $$

Подставив в соответствующие формулы конкретные значения из условия задачи $a = 30; b = 40; c = 14; m = 3; n = 4$ получил:

$$h = \frac{30\cdot{40}\cdot{14}}{\sqrt{(30+40+14)(-30+40+14)(30-40+14)(30+40-14)}}=25$$

$$v = \frac{2\cdot{25}\cdot{14}}{(4 - 3)\sqrt{4\cdot25^2-14^2}} = 175/12$$

Это скорость в mph(милях в час). Таким образом, данные о 12-ти, 13-ти и 14 часах избыточны. Полагаю, достаточно было просто сказать, что в три определённых момента времени(не важно каких) все корабли были на одинаковом расстоянии от маяка.

Обсуждение

Наконец-то, Марафон внес свой вклад в решение задачи трех тел. Осталось всего ничего: изменить размерность, учесть гравитацию...


Я испытывал некоторые затруднения при "раздаче слонов".
Правильно ли давать автору задачи столько же баллов, чем тому, кто ее всего лишь решил?
Заглянул в архивы. И нашел как подтверждение (ММ72), так и опровержение этого тезиса (ММ43). Однако во втором случае в авторском решении нашлось некое углубление задачи.
Еще сложнее, было оценить решение Антона Никонова.
С одной стороны, он существенно обобщил задачу.
С другой стороны, его решение нерационально.
С третьей (или снова с первой?) стороны, героический труд должен быть как-то оценен.
С четвертой (или снова со второй?) стороны, этот героический труд во многом был проделан еще при обобщении ММ186...
Итог моих сомнений отражен в следующем разделе.

Награды

За составление задачи ММ196 Олег Полубасов получает 9 призовых баллов. За решение и обобщение задачи Антон Никонов и Константин Кноп получают по 10 призовых баллов, а Виктор Филимоненков, Сергей Половинкин, Ариадна, Анатолий Казмерчук и Дмитрий Пашуткин - по 9 призовых баллов.

Эстетическая оценка задачи - 4.8 балла

[Masik]

VAL в сообщении #922788 писал(а):

Авторское решение Олега Полубасова приведу в отдельном сообщении.

Не понятно, за что такая дискриминация? Мне казалось, что авторское решение должно было быть приведено в первую очередь.
И зачем некоторым участникам потребовалось стрелять из пушки по воробьям? Я же сразу предупредил, что задача простая.

[VAL]

Masik в сообщении #922818 писал(а):

VAL в сообщении #922788 писал(а):

Авторское решение Олега Полубасова приведу в отдельном сообщении.

Не понятно, за что такая дискриминация? Мне казалось, что авторское решение должно было быть приведено в первую очередь.

Почему сразу дискриминация?!
Может, наоборот, привилегия!?

Хотя, на самом деле ни то, ни другое. Просто на форуме есть ограничение - не более трех вложений в одном сообщении.
Поэтому, все равно, пришлось бы какое-то из решений приводить отдельно. Поскольку три остальных формально равноправны, я решил выделить авторское.

Цитата:

И зачем некоторым участникам потребовалось стрелять из пушки по воробьям? Я же сразу предупредил, что задача простая.

Ну, например, для того, чтобы продемонстрировать наличие пушки.
Хотя более вероятным представляется объяснение: воробьев издали приняли за стратегические бомбардировщики.

Да, чуть не забыл!

Вложение:

Комментарий к файлу: Решение Олега Полубасова
MM196_Полубасов.pdf [311.73 Кб]
Скачиваний: 485

[VAL]

===========ММ197===============

ММ197 (5 баллов)

Будем говорить, что n-угольник относится к классу k, если его можно разрезать на k треугольников одной прямой и нельзя разрезать одной прямой на большее число треугольников. Найти все возможные значения k для $n = 2014$.

Примечания:
1. Никаких других фигур при разрезании возникать не должно.
2. Если вышеописанный разрез осуществить нельзя, многоугольник относится к классу 0.

Решение

Привожу только одно решение ММ197, поскольку остальные правильные решения идентичны приведенному.

Вложение:

Комментарий к файлу: Решение Олега Полубасова
MM197_Полубасов.pdf [203.86 Кб]
Скачиваний: 510

Обсуждение

К моему удивлению, эта задача, представлявшаяся мне достаточно простой, вызвала затруднения даже у некоторых "зубров" Марафона.
Не все участники догадались, что линия разреза может целиком содержать некоторые стороны многоугольника.
Другие не заметили, что крайние точки разреза могут быть как вершинами, как и внутренними точками сторон.
За еще одну потерю (случай $k=0$) я оценку не снижал, поскольку в первоначальном варианте условия (не приводившем к классификации n-угольников) этот случай не возникал, а часть решений поступила еще до уточнения условия.

Дополнительный балл начислен Олегу Полубасову за некое обобщение задачи. Аналогичное обобщение есть в решении Владимира Дорофеева, но его дополнительный балл "сократился" с баллом изъятым за погрешности в изложении решения.

Награды

За решение задачи ММ197 участникам начислены следующие призовые баллы:
Олег Полубасов получает - 6;
Константин Хадаев, Виктор Филимоненков, Владимир Дорофеев, Сергей Половинкин и Дмитрий Пашуткин - по 5;
Ариадна - 4;
Анатолий Казмерчук - 2;
Антон Никонов - 1;,

Эстетическая оценка задачи - 4.9 балла

[VAL]

Текущее положение участников в XX туре Математического марафона
\begin{tabular}{|l|l|r|r|r|r|r|r|r|r|r|r|} \hline №& Участники& 191 & 192 & 193 & 194 & 195 & 196 & 197 & \Sigma \\ \hline & \textit{Номинал задачи} & \textit{4} & \textit{5} & \textit{6} & \textit{6} & \textit{7} & \textit{9} & \textit{5} & \textit{42} \\ \hline 1.& Олег Полубасов & 5 & 5 & 6 & 6 & 10 & 9 & 6 & 47 \\ \hline 2.& Виктор Филимоненков & 4 & 5 & 6 & 6 & 7 & 9 & 5 & 42 \\ \hline 3.& Ариадна & 4 & 5 & 6 & 6 & 7 & 9 & 4 & 41 \\ \hline 3.& Сергей Половинкин & 5 & 4 & 5 & 6 & 7 & 9 & 5 & 41 \\ \hline 3.& Дмитрий Пашуткин & 4 & 4 & 6 & 6 & 7 & 9 & 5 & 41 \\ \hline 6.& Антон Никонов & 4 & 5 & 5 & 6 & 9 & 10 & 1 & 40 \\ \hline 7.& Анатолий Казмерчук & 4 & 5 & 6 & 6 & 7 & 9 & 2 & 39 \\ \hline 8.& Константин Хадаев & 4 & 2 & 4 & 6 & 7 & - & 5 & 28 \\ \hline 9.& Владимир Дорофеев & 4 & - & 6 & - & - & - & 5 & 15 \\ \hline 10.& Константин Кноп & - & - & - & - & - & 10 & - & 10 \\ \hline 11.& Николай Дерюгин & 4 & - & - & - & - & - & - & 4 \\ \hline 12.& Денис Артюшин & 3 & - & - & - & - & - & - & 3 \\ \hline \end{tabular}

[Masik]

VAL в сообщении #925336 писал(а):

Текущее положение участников в XX туре Математического марафона

Владимир, спасибо за интересные задачи! А можно, чтобы в таблицах всегда была строка "цена задачи" или "номинал", в общем, ватерлиния, по которой можно ориентироваться?

[VAL]

Masik в сообщении #925403 писал(а):

А можно, чтобы в таблицах всегда была строка "цена задачи" или "номинал", в общем, ватерлиния, по которой можно ориентироваться?

Можно. И даже не сложно.

[Masik]

VAL в сообщении #925418 писал(а):

Masik в сообщении #925403 писал(а):

А можно, чтобы в таблицах всегда была строка "цена задачи" или "номинал", в общем, ватерлиния, по которой можно ориентироваться?

Можно. И даже не сложно.

Спасибо. А заполните, пожалуйста, и поле "сумма".

[Yadryara]

Позвольте всё же спросить публично, ибо задача уже может обсуждаться.

VAL в сообщении #925336 писал(а):

Будем говорить, что n-угольник относится к классу k, если его можно разрезать на k треугольников одной прямой и нельзя разрезать одной прямой на большее число треугольников.

Выделение моё. Я так понял, выделенное означает, что надо искать именно максимум. А он для 2014-угольника только один и равен $1008$.

И эта задача отлична от такой:

Вопрос:
На какое количество треугольников можно разрезать 2014-угольник одной прямой?

Ответ:
Если можно, то на любое от $672$ до $1008$ включительно.

VAL в сообщении #925003 писал(а):

Не все участники догадались, что линия разреза может целиком содержать некоторые стороны многоугольника.

Догадался.

VAL в сообщении #925003 писал(а):

Другие не заметили, что крайние точки разреза могут быть как вершинами, как и внутренними точками сторон.

Заметил. Вот моё решение в миниатюре.

$\tikz[scale=.5]{\draw(0,0)--(1,1)--(0,3)--(2,3)--(1,2)--(2,0)--(0,0) \draw(5,0)--(6,1)--(5,2)--(6,3)--(5,5)--(7,5)--(6,4)--(7,3)--(6,2)--(7,0)--(5,0) \draw(10,0)--(11,1)--(10,2)--(11,3)--(10,4)--(11,5)--(10,7)--(12,7)--(11,6)--(12,5)--(11,4)--(12,3)--(11,2)--(12,0)--(10,0) \draw(1,0)--(1,3)[green]\draw(6,0)--(6,5)[green]\draw(11,0)--(11,7)[green]}$

Представлены 6-ти, 10-ти и 14-угольники. Количество треугольников, полученных после разрезания по зелёной линии, соответственно — 4, 6 и 8.

Нетрудно видеть, что количество треугольников для таких чётно-нечётных $n$ равно

$$\frac{n}2+1$$

Поскольку число $2014$ тоже чётно-нечётное, вполне можно построить 2014-угольник и разделить его на $\frac{2014}2+1= 1008$ треугольников.


Сразу скажу, что задача обязательно поучаствовать в решении всех марафонских задач не ставилась. Скорее всего, по целому ряду причин, я, видимо, не смогу продолжить участие в нынешнем туре.

Зато у меня будет больше времени написать на другие темы, в том числе о других задачах нашего уважаемого автора.

[VAL]

Yadryara в сообщении #927284 писал(а):

Позвольте всё же спросить публично, ибо задача уже может обсуждаться.

Без проблем.

VAL в сообщении #914787 писал(а):

Надеюсь, что уточненная формулировка устранит возможные кривотолки:

Как говорится "Надежды юношей питают...". Увы

Для удобства дальнейшего обсуждения привожу все условие, а не только фрагмент:

Цитата:

ММ197 (5 баллов)

Будем говорить, что n-угольник относится к классу k, если его можно разрезать на k треугольников одной прямой и нельзя разрезать одной прямой на большее число треугольников. Найти все возможные значения k для $n = 2014$.

Примечания:
1. Никаких других фигур при разрезании возникать не должно.
2. Если вышеописанный разрез осуществить нельзя, многоугольник относится к классу 0.

Yadryara писал(а):

VAL в сообщении #925336 писал(а):

Будем говорить, что n-угольник относится к классу k, если его можно разрезать на k треугольников одной прямой и нельзя разрезать одной прямой на большее число треугольников.

Выделение моё. Я так понял, выделенное означает, что надо искать именно максимум. А он для 2014-угольника только один и равен $1008$.

А выделение синим - мое.
Для каждого конкретного 2014-угольника искомое k - единственное. Но для 2014-угольников возможных k много.

Для чего в условии присутствует выделенное Вами?
Для того, чтобы исключить ситуацию, когда один и тот же многоугольник относится сразу к нескольким классам (само употребление слова "класс" обязывает).
Например, невыпуклый четырехугольник, очевидно, можно разрезать одной прямой и на 2, и на 3 треугольника.

Yadryara писал(а):

VAL в сообщении #925003 писал(а):

Не все участники догадались, что линия разреза может целиком содержать некоторые стороны многоугольника.

Догадался.

VAL в сообщении #925003 писал(а):

Другие не заметили, что крайние точки разреза могут быть как вершинами, как и внутренними точками сторон.

Заметил.

Тем обиднее

Yadryara писал(а):

Сразу скажу, что задача обязательно поучаствовать в решении всех марафонских задач не ставилась. Скорее всего, по целому ряду причин, я, видимо, не смогу продолжить участие в нынешнем туре.

Не в силах Вам запретить
Но, на мой взгляд, сход с дистанции после первой же относительной неудачи - это неспортивное поведение
Тем более, что большая часть тура пройдена и суммарный результат пока вполне конкурентоспособен.

Цитата:

Зато у меня будет больше времени написать на другие темы, в том числе о других задачах нашего уважаемого автора.

Здесь я только "за".