Диафантовое уравнение

[iskander9908]

Приветствую форумчане,

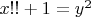
Я пытаюсь найти способы для поиска решений уравнения $x!! + 1 = y^2$ в целых числах.

Пытался рассмотреть разные случаи: когда $x$ - чётное и когда нечётное, но ничего путного не добился. Для
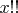
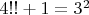
четных $x$ я получил, что $x!!$ представим в произведении двух последовательных чётных чисел. Была идея, что это возможно только при $x = 4$ ($4!! + 1 = 3^2$), но не смог доказать что двойной факториал не может быть представлен в виде произведения двух последовательных чётных чисел, если он не равен $4$. Поэтому задумался: есть ли какая-нибудь теория, которая сможет отсеять ненужные решения?

P.S. - проверив на компьютере значения до $2000$, нашёл только $3,4,5,6$.

[waxtep]

Не уверен, что поможет, но 10 лет назад обсуждали задачу подобного типа здесь:

scwec в сообщении #1134681 писал(а):

П.Эрдёш и Р.Облат в 1937 году доказали в частности, что уравнение $n!\pm{1}=k^p$, для $n>2$ и нечетных простых $p$ решений не имеет (доказательство не простое)