Непривычно...

[pavelyoung]

Здравствуйте! Недавно начал изучать математический анализ - однако странное чувство:
Вроде все понимаю [почти], но чувствую себя 'не в своей тарелке'. Это нормально? Извиняюсь, если вопрос окажется глупым, но все же. Включил в раздел 'околонаучные темы', так как это больше не про сами математические задачи, а тема другого рода

[Mihaylo]

Может не видно света в конце туннеля? Вроде как понятно, почему так шагаем, но зачем?

[EUgeneUS]

pavelyoung в сообщении #1713084 писал(а):

Вроде все понимаю [почти], но чувствую себя 'не в своей тарелке'. Это нормально?

1. Если после усвоения материала Вы можете решать задачи к пройденному материалу, то это нормально.
1.1. Если в этом случае ощущение "ненормальности" сохраняется, то это связано с тем, возможно, что мыслительные усилия для Вас не являются нормой. Это не страшно. Продолжайте тренировки.

2. Если после усвоения материала Вы не можете решать задачи к пройденному материалу, то это ненормально.
2.1. Если в этом случае имеется ощущение "ненормальности", то оно Вас не подводит.

[pavelyoung]

Спасибо! Вроде иногда понимаю, иногда нет. Например интегралы (не сильно сложные) умею решать :
$\int xe^{x} dx$
$\int x^2 \sin x dx$
И подобные... Однако бывало смотрю лекцию: и не понимаю, например зачем делать замену переменной используя гиперболический синус, если он вообще не в тему (вроде бы такой интеграл был) :

$\int \dfrac{1}{\sqrt{1+x^2}} dx$

[EUgeneUS]

pavelyoung в сообщении #1713142 писал(а):

Однако бывало смотрю лекцию: и не понимаю, например зачем делать замену переменной используя гиперболический синус, если он вообще не в тему

Хмм.
А в таких случаях попробуйте найти первообразную без замены, которая показалось "странной" и "не нормальной".

[Dedekind]

pavelyoung в сообщении #1713142 писал(а):

зачем делать замену переменной используя гиперболический синус, если он вообще не в тему (вроде бы такой интеграл был) :

Почему не в тему? Основное тригонометрическое тождество же. Если $1-x^2$ - то обычный синус. Если $1+x^2$ - гиперболический.

[EUgeneUS]

Кстати,

Цитата:

Элементарные функции — это функции, которые можно получить из основных элементарных функций (степенной, показательной, логарифмической, тригонометрических и обратных тригонометрических) с помощью конечного числа арифметических операций (сложение, вычитание, умножение, деление) и композиции (суперпозиции).

Дифференцирование и интегрирование (в смысле нахождения первообразной) - операции обратные. Но существует такая асимметрия:
1. Производная любой элементарной функции - есть элементарная функция.
2. А первообразная элементарной функции совсем не обязана быть элементарной функцией.

Поэтому для интегрирования используются разные методы, каждый из которых не для всех случаев подходит, а только для некого класса функций.
А для каких-то функций не подходит никакой метод. Тогда приходится вводить специальные функции.

[pavelyoung]

Возможно, рано изучать мне эту тему, но как доказывают, что интеграл от некой функции не выражаются в элементарных? Просто вдруг существует какой-то метод, с помощь которого можно решить некоторые интегралы, которые обычными методами не выйдет найти?

[EUgeneUS]

pavelyoung
Некоторые, важные в прикладном смысле, случаи исследованы, и результаты таких исследований известен.
Например, эллиптические интегралы.

[b4b5]

pavelyoung Интегрирование - это набор "лайфхаков" в значительной степени.

[mihaild]

pavelyoung в сообщении #1713150 писал(а):

Возможно, рано изучать мне эту тему, но как доказывают, что интеграл от некой функции не выражаются в элементарных?

Не то чтобы рано, это материал ИМХО примерно того же уровня сложности, что и интеграл Римана. Неплохое изложение, например, здесь. Но это требует думать о производной как о просто абстрактной операции, а не о чем-то, без связи с топологией (например с пределами). И обычно не является частью стандартных курсов.

pavelyoung в сообщении #1713150 писал(а):

Просто вдруг существует какой-то метод, с помощь которого можно решить некоторые интегралы, которые обычными методами не выйдет найти?

"Решить интеграл" - на мой взглляд, крайне неудачный жаргон. Есть понятие "выразить первообразную в элементарных функциях". Тут полезный инструмент для доказательства невозможности - теорема Лиувилля.
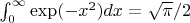
А еще есть понятие "найти значение определенного интеграла". И тут бывает, что первообразная в элементарных функциях не выражается, а вот значение интеграла - выражается. Например $\int_0^\infty \exp(-x^2) dx = \sqrt{\pi} / 2$, но первообразная от $\exp(-x^2)$ в элементарных функциях не выражается.
Для такого нахождения есть много разных интересных инструментов, часть из них будет в курсе математического анализа, часть - возможно внезапно - в курсе комплексного анализа.

[dgwuqtj]

pavelyoung в сообщении #1713142 писал(а):

не понимаю, например зачем делать замену переменной используя гиперболический синус, если он вообще не в тему

Просто куча методов вычисления интегралов является трюками. Их студенты запоминают (путём решения задач), но какой-то единой красивой теории за этим нет.

pavelyoung в сообщении #1713150 писал(а):

как доказывают, что интеграл от некой функции не выражаются в элементарных?

А это, как и "общие" алгоритмы вычисления интегралов (без трюков, но для человека неудобно и вычислительно сложно), в университетский курс не входит. И вообще это уже не матанализ, а дифференциальная алгебра.

[Mihaylo]

dgwuqtj в сообщении #1713159 писал(а):

Просто куча методов вычисления интегралов является трюками. Их студенты запоминают (путём решения задач), но какой-то единой красивой теории за этим нет.

Подтверждаю. Но я бы хотел мотивировать: несмотря на отсутствие красивой теории, выучивание тех самых трюков ведёт к развитию мышления, успешной учёбе и успешной дальнейшей карьере. Но и увлекаться этим не стОит, часы изучения интегралов не принесут миллиардов. Но хотя бы решите те интегралы, которые заданы. Очень много интегралов - это игры типа олимпийских. Быть чемпионом - это обычно не показатель, но круто, да.

[lel0lel]

Решай интеграл!
Производную тоже решай!
Не стремись к миллиардам
О них вообще не мечтай!
Мышление развито будет на пять
И сразу начнёшь интеграл вычислять