Вдогонку к задаче
DimaM topic161569.html, придумал свою: на какую высоту

поднимется вода в тонком стеклянном капилляре, если сверху эта трубка запаяна? Смачивание считать полным. Коэффициент поверхностного натяжения

; внутренний радиус капилляра

; ускорение силы тяжести

; атмосферное давление
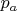
; длина трубки

.
В процессе решения получается квадратное уравнение относительно

, причем, оба корня вроде как положительные. Выбирать меньший из них, следуя принципу минимума энергии Гиббса?