Дайте дорогу актуальной бесконечности

[Altenter]

Ende
Выделено из темы «Гипотеза о симметричных простых близнецах»

Ryzl в сообщении #1706547 писал(а):

Altenter в сообщении #1706546 писал(а):

Ryzl в сообщении #1706545 писал(а):

При каком значении вероятности в математике можно принимать событие как невозможное?

0.

А если при N-> бесконечности вероятность -> 0 не канает?

Ну это же не означает, что она 0 на конечном интервале? Она может не от нуля ведь стремиться, а от 1, например.

-- 20.10.2025, 18:47 --

mihaild в сообщении #1706548 писал(а):

Altenter в сообщении #1706546 писал(а):

0.

Более точно: вероятность невозможного события $0$, но не всякое событие нулевой вероятности невозможно.

Да, согласен. Что на шестигранном кубике выпадеть седьмая грань - невозможное событие с нулевой вероятностью, а что при счетном количестве подбрасываний шестигранного кубика будут всегда выпадать шестерки - возможное событие нулевой вероятности. (На самом деле т.к. актуальной бесконечности нет, то и это событие невозможно, либо извините, подвинтесь и дайте дорогу актуальной бесконечности).

[mihaild]

Altenter в сообщении #1706549 писал(а):

т.к. актуальной бесконечности нет

Нельзя сказать, что "нет актуальной бесконечности", потому что нет такого понятия.
Невозможное событие - пустое множество элементарных исходов. Никакой философии про "актуальную бесконечность", просто тривиальное определение, удобное в некоторых случаях.

[Altenter]

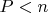
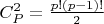
Здесь можно рассуждать так: Количество простых чисел возрастает с замедлением, Т.е. у нас есть более-менее правдоподобная оценка количества простых $P< n$, они образуют $C_P^2=\frac{p!(p-1)!}{2}}$ пар. Все. Ничего об этих парах мы сказать не можем, кроме того, что их центры в интервале от 5 до n. Очевидно, что у некоторых пар их центр совпадает.

-- 20.10.2025, 19:04 --

mihaild в сообщении #1706551 писал(а):

Altenter в сообщении #1706549 писал(а):

т.к. актуальной бесконечности нет

Нельзя сказать, что "нет актуальной бесконечности", потому что нет такого понятия.
Невозможное событие - пустое множество элементарных исходов. Никакой философии про "актуальную бесконечность", просто тривиальное определение, удобное в некоторых случаях.

Красиво, но Вы сначала докажите, что для счетного множества исходов, раз уж Вы берете непустое счетное множество исходов с одним благоприятным исходом, применимы формулы теории вероятностей.

-- 20.10.2025, 19:09 --

А я пока тем временем докажу, что они неприменимы: Т.к., что мы возьмем 2 благоприятных исхода, что 3, что 100 или 10^100 из счетного множества, результат будет один и тот же:0, ну и как это соотносится с формулой для вероятности благоприятного исхода? Там в ней должно в знаменателе быть N, чтобы она могла быть применена, а не счетное множество.

[mihaild]

Altenter в сообщении #1706552 писал(а):

Красиво, но Вы сначала докажите, что для счетного множества исходов, раз уж Вы берете непустое счетное множество исходов с одним благоприятным исходом, применимы формулы теории вероятностей

Создайте отдельную тему, в которой напишите конкретные формулы, приведите свои попытки их вывода, укажите, в чём затруднения, и я Вам подскажу, как их выводить.

[Altenter]

(Оффтоп)

mihaild в сообщении #1706553 писал(а):

Altenter в сообщении #1706552 писал(а):

Красиво, но Вы сначала докажите, что для счетного множества исходов, раз уж Вы берете непустое счетное множество исходов с одним благоприятным исходом, применимы формулы теории вероятностей

Создайте отдельную тему, в которой напишите конкретные формулы, приведите свои попытки их вывода, укажите, в чём затруднения, и я Вам подскажу, как их выводить.

Так и ежу понятно, пополните натуральный ряд бесконечностью, т.е. по сути используете понятие актуальной бесконечности и приравняете результат деления натурального числа на нее нулю.
Иначе у Вас как у Бора:

Цитата:

У Бора электрон не квантуется по пятницам, а в соответствии с его постулатами, существует в стационарных состояниях с определённой энергией, не излучая её.

А злой я такой -так это потому, что у меня велосипеда нет!

[Ende]

Altenter в сообщении #1706554 писал(а):

Так и ежу понятно, пополните натуральный ряд бесконечностью, т.е. по сути используете понятие актуальной бесконечности и приравняете результат деления натурального числа на нее нулю.

Altenter
Недельный бан за невежественные ответы в чужой теме и клевету на ежей.