хочу разобраться с CPT

[Cos(x-pi/2)]

Да, в основном Вы правильно рассуждаете. (О координатах частиц не будем заботиться, они роли не играют: они изменяются из-за движения частиц, да и на саму такую картину реакции можно смотреть ведь под разными углами и с разным выбором начала отсчёта координат; так что, координаты оставим без внимания).

Вот, схематично нарисовал, о чём идёт речь:



В нашем упрощённом примере будем считать, что масса нейтрино равна нулю. (Из опытов следует, что масса нейтрино может быть очень маленькой отличной от нуля величиной, но не будем здесь усложнять картину этим нюансом).

Из теории относительности следует, что частица с равной нулю массой всегда должна двигаться со скоростью света, а спин у неё может быть направлен только либо вдоль её вектора импульса, либо в направлении противоположном её импульсу.

В этом сюжете надо знать ещё некоторые факты из физики элементарных частиц - знать, какими харатеристиками частицы описываются, и какие законы сохранения должны выполняться. Частица $\pi^+$ имеет электрический заряд, равный абсолютной величине заряда электрона, его принято выбирать за единицу электрического заряда $(+1).$ Другие её заряды, такие как барионный и разновидности лептонного числа, - равны нулю.

Мюон и мюонное нейтрино это лептоны, обе эти частицы имеют мюонное лептонное число (считайте, что это не электрическая разновидность заряда) $L_{\mu}$ равное $+1.$ У их античастиц этот заряд противоположен по знаку. Это общее свойство для всех видов зарядов: заряды частиц и их античастиц противоположны. Электрический заряд мюона $\mu^-$ такой же, как у электрона: $(-1).$ У нейтрино электрический заряд равен нулю.

В реакциях строго сохраняется электрический заряд; поэтому положительно заряженная частица $\pi^+$ не может превратиться в отрицательный мюон $\mu^-$ (с мюонным антинейтрино $\bar{\nu}_{\mu}),$ а превратиться в антимюон $\mu^+$ с мюонным нейтрино $ \nu_{\mu}$ может.

Кроме того, лептонный заряд сохраняется; в данном примере это мюонное лептонное число. Поэтому из частицы $\pi^+$ с нулевым лептонным числом если и могут образовываться лептоны, то только парами - с противоположными знаками лептонного числа.

Ну и "кинематические заряды" сохраняются - момент импульса (в нашем упрощённом до классической наглядности примере это суммарный вектор спина), и сам импульс (суммарный вектор импульса). И энергия сохраняется, но это никак не показать на рисунке. Вообще эти величины, "кинематические" переменные , не принято называть "зарядами", и лучше их так не называть, чтобы не было путаницы с постоянными зарядами частиц.

Вот с такой точки зрения ещё поразглядывайте рисунок - как там выполняются перечисленные законы сохранения; в том числе и в зеркальной реакции, которая на практике не наблюдается.

Может быть, если ещё кое-что знаете из физики элементарных частиц в дополнение к сказанному, то и сумеете ответить на вопрос, почему показанной на рисунке зеркальной реакции нет в природе. (И для физиков в своё время это было загадкой!) Попозже напишу ответ.

--------
P.S.:
upd: исправил внизу на рисунке знаки неравенств для скалярных произведений $\vec{s}\cdot\vec{p}.$

[hurt]

Cos(x-pi/2)
что меня смущает на картинке при инверсии P, есть такое понятие как хиральность - я представляю это как фундаментальное свойство частицы определяющее ее поведение, но это свойство я могу понять лишь через математический аппарат, поэтому для меня хиральность, как не математика в самом обыщем смысле это больше абстракция.
Но нужно понимать что отраженный на правой стороне изображения нейтрино имеет общее направление векторов спина и импульса- такого просто быть не может т.к. совпадение векторов указывает на то, что получившийся нейтрино правохиральный , но нейтрино может быть лишь левохиральным -приходим к парадоксу.
А вот для антимюон $\mu^+$ в плане однонаправленности векторов кажется все сходится частица может быть правохиральной.

Если к этому всему добавить то что Вы описали о зарядах и их несовпадении с родительской частицей мезон $\pi^+$. Получается реакция распада просто не может произойти, но если частица не может находится в стабильном состоянии тогда как этот вопрос решает Вселенная, не математически, а буквально на физическом уровне?

[Cos(x-pi/2)]

hurt в сообщении #1706663 писал(а):

Если к этому всему добавить то что Вы описали о зарядах и их несовпадении с родительской частицей мезон $\pi^+$. Получается реакция распада просто не может произойти,

Так ведь нет никакого несовпадения зарядов. Как раз законы сохранения зарядов выполняются - и на исходной картинке (где нарисован существующий распад), и на зеркальной (где нарисован несуществующий распад). Я написал, что электрически отрицательно заряженная частица $\pi^-$ не может превратиться в положительно заряженный мюон $\mu^+$ (т.е. в антимюон по отношению к отрицательному мюону $\mu^-).$ Написал об этом просто для примера того, как закон сохранения (в данном примере это закон сохранения электрического заряда) может запрещать некоторые реакции. Ну или я не понял Вас, и говорю сейчас не о том, о чём сказали Вы.

Насчёт "хиральности" Вы правильно нашли ответ. Сейчас закончу очередной рисунок и поясню это подробнее. А пока следующая Вам задачка такая: попробуйте теперь применить к той несуществующей реакции зарядовое сопряжение C. Если сделать это правильно, то получится описание другой реакции - и она, оказывается, существует: она обнаруживается на самом деле в экспериментах.

[hurt]

Cos(x-pi/2)
так давайте посмотрим что произойдет при изменении CP
1) и так есть мезон $\pi^+$ находится в состоянии покоя меняем CP из CPT - меняется знак заряда получаем $\pi^-$, происходит изменение знака импульса, но он равен 0 так что ничего не изменится

2) далее частица распадается, в итоге мы получаем отрицательный мюон и мюонное антинейтрино, при этом получается, что знак заряда у мюон отрицательный, а антинейтрино 0, а вектора если я верно понимаю будут такими же как и при предыдущем результате распада без изменения C.

Таким образом получается, что антинейтрино имеет правую спиральность , как Вы писали ранее -у нейтрино электрический заряд равен нулю, значит и антинейтрино имеет 0-вой заряд, это кстати объясняет почему $\bar{\nu}_{\mu},$ пишется так. Т.е. по итогу антинейтрино сошлось.

Что касается мюона он получает отрицательный заряд мюон $\mu^-$ , а вектор импульса и спина будут противоположны или направлены в одну сторону? Как я понял для $\mu^-$ направленность векторов может быть любой. Что в целом допускает существование такой частицы.

И здесь настает момент, когда я должен спросить, но Cos(x-pi/2) , при первом опыте с инверсией P мы же получили то же самое нейтрино, а Вы вероятно ответите , но лептонный заряд описанный ранее для нейтрино меняется, а "истинный" антинейтрино должен иметь лептонный заряд -1 что и произошло. И это объясняет почему такая процедура распада возможна в текущем эксперименте и невозможна в первом при смене одного P.
И как оказалось этот второй процесс называется допустимым слабым распадом

[Cos(x-pi/2)]

hurt

Да, Вы всё верно говорите.

Но поскольку я успел написать длинное продолжение пояснений, прежде чем увидел сейчас Ваш текст, то всё-таки с Вашего позволения помещаю свои пояснения ниже (ну, жалко ведь их выбрасывать :)


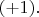
"Хиральность" или, что то же самое, спиральность нейтрино можно понимать просто-напросто как термин, описывающий знак проекции спина на направление импульса. Если спин $\vec{s}$ и импульс $\vec{p}$ направлены в одну и ту же сторону, то упомянутая проекция положительная, и спиральность считается равной $(+1).$ Если же спин $\vec{s}$ и импульс $\vec{p}$ направлены в противоположные стороны, то указанная проекция получается отрицательной, и спиральность считается равной $(-1).$

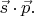
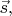
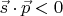
Математически знак проекции этих векторов друг на друга определяется знаком их скалярного произведения $\vec{s}\cdot\vec{p}.$ У меня на рисунках показаны и сами векторы $\vec{s},$ $\vec{p},$ и знаки их скалярных произведений - эти неравенства фактически указывают спиральность. 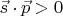А именно: на рисунках у нейтрино с $\vec{s}\cdot\vec{p}<0$ спиральность равна $(-1),$ а в случае с $\vec{s}\cdot\vec{p}>0$ спиральность равна $(+1).$

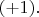
Поскольку векторы $\vec{s}$ и $\vec{p}$ на рисунках изображены, и глазами прямо видно, как они направлены, то мы можем даже вообще не упоминать этот сильно научный термин "спиральность", а прямо так картинками всё и пояснять.

Так вот. Когда-то давным-давно физики думали, что все взаимодействия элементарных частиц характеризуются "P-симметрией", т.е. все они "зеркально-симметричны". Эти слова для нашего примера означают вот что: если с какой-то не равной нулю вероятностью в реакциях рождается нейтрино $\nu_{\mu}$ c противоположно направленными $\vec{s}$ и $\vec{p},$ то с такой же вероятностью должно рождаться и нейтрино с одинаково направленными $\vec{s}$ и $\vec{p}.$ Потому что эти две картинки переходят друг в друга при зеркальном отражении; другими словами: они переходят друг в друга под действием P-преобразования, что и показано у нас на рисунках.

Но природа распорядилась по-своему. Оказалось, что в природе запрещено существовать таким нейтрино, у которых $\vec{s}$ и $\vec{p}$ направлены одинаково. Этот удивительный экспериментальный факт физики назвали "нарушением P-симметрии".

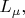
Но это ещё не всё. Оказалось, что природа разрешает существовать частицам, похожим на нейтрино с одинаково направленными $\vec{s}$ и $\vec{p},$ но только такие частицы ведут себя в реакциях не как нейтрино, а как антинейтрино. Т.е. 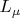надо считать, что у них есть так называемый лептонный заряд (другое его название - лептонное число) $L_{\mu},$ и он имеет противоположный знак по сравнению с лептонным зарядом $L_{\mu}$ тех нейтрино, у которых $\vec{s}$ и $\vec{p}$ направлены противоположно друг друг другу. Если так считать, и полагать, что лептонный заряд в реакциях сохраняется, то получалось очень хорошее согласие с наблюдениями многих других реакций. В том числе, получалось согласие с наблюдением отсутствия ряда реакций, которые раньше казались теоретически возможными; просто они оказались запрещёнными законом сохранения лептонного заряда.

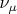
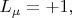
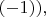
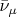
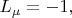
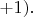
Таким образом, физикам пришлось принять как экспериментальный факт, что существуют нейтрино $\nu_{\mu}$ с $L_{\mu}=+1,$ c противоположно направленными $\vec{s}$ и $\vec{p}$ (спиральность $(-1)),$ и существуют антинейтрино $\bar{\nu}_{\mu}$ с $L_{\mu}=-1,$ c одинаково направленными $\vec{s}$ и $\vec{p}$ (спиральность $+1).$ И поменять в этом описании направления $\vec{s}$ и $\vec{p}$ нельзя, иначе получится описание несуществующих частиц.

Теперь введём в дело операцию С (так называемое зарядовое сопряжение) следующим простейшим способом: положим, что эта операция никак не влияет на $\vec{s}$ и $\vec{p},$ а только изменяет на противоположные знаки всех зарядов - и электрических и лептонных.

Ниже на рисунке в правой части показан результат применения С к частицам в описании той самой несуществующей реакции (оно показано в левой части рисунка), которая получилась из первоначальной реакции операцией Р.



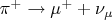
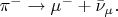
Таким образом, применение последовательности операций Р и С к описанию существующей исходной реакции $\pi^+\to \mu^+ +\nu_{\mu}$ привело нас к описанию реакции $\pi^-\to \mu^- +\bar{\nu}_{\mu}.$ Оказывается, такая реакция существует и притом реализуется в опытах с такой же вероятностью, что и исходная реакция.

Такого рода примеры позволили физикам тогда сказать, что взаимодействия частиц характеризуются "CP-симметрией".

Преобразование Т мы можем ввести в рассмотрение просто как перемену местами начальных и конечных частиц в реакциях. Если вдаваться в подробности, то Т ещё и меняет направления $\vec{s}$ и $\vec{p}$ на противоположные - все движения, и вращательное и поступательное, после Т происходят в обратных направлениях; спиральность при этом не меняется.

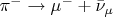
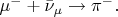
Тем самым получается описание обратных реакций. Например, применив Т к последней нашей картинке, получим вместо описания распада $\pi^-\to \mu^- +\bar{\nu}_{\mu}$ описание реакции образования одной частицы из двух: $\mu^- +\bar{\nu}_{\mu}\to \pi^-.$ Такие реакции, обратные к исходным, не запрещены, и, значит, "СРТ-симметрия" не нарушена. (Хотя осуществить обратные реакции в опытах может быть трудно - надо "прицеливаться" одной частицей в другую, чтобы они вступили в реакцию друг с другом).

Дальше не знаю что: можно либо другие подобные примеры разбирать, либо пытаться разобрать хотя бы частично намного более тяжёлый сюжет - о нарушении CP-симметрии; и совсем малоподъёмное дело - разбирать, как вся эта эмпирика учитывается в математическом формализме моделей КТП. Вы решайте, есть ли у Вас ещё вопросы для форума, и какие, или дальше будете по книгам и статьям разбираться.

[hurt]

Cos(x-pi/2) ну по первых большое спасибо за этот эксперимент и серию наводящих вопросов.
да действительно совсем малоподъёмное дело - разбирать, как вся эта эмпирика входит в матматический формализм КТП

понимаете я пытался разобраться чем является Т в CPT я понимаю, что это оператор обращения времени. Я понимаю что CPT ,сама теорема, это гарантия фундаментальной согласованности физической теории и любая локальная квантовая теория поля должна быть инвариантной относительно одновременного применения трёх преобразований.
Но возникла одна проблема- время буквально не идет вспять) и согласно стандартной Квантовой Теории Поля не допускается движение времени назад, как я понял это просто не допустимо в том мат аппарате который использует КТП.
При этом CPT появилась благодаря КТП , CPT буквально создана что бы быть гарантом стабильности теории - любая локальная теория поля должна следовать принципу CPT.
И в этом и заключается парадокс если в КТП вектор времени назад не возможен, почему в CPT появляется оператор обращения времени )))))

Сама по себе эта ситуация что это?

На уровне математики меняется вектор времени, на уровне физических процессов нашего времени это изменение Т сводится к тому что для частицы, как я понимаю(поправьте если ошибаюсь) на уровне квантового поля происходит изменение "программы" описывающей поведение(как она должна взаимодействовать с другими частицами) инвертированной частицы. Но тогда логичным было бы создать не CPT теорему, а что то вроде CP + изменение поведения частиц для стабилизации частицы при измененном CP -как то бы так она называлась.
Но авторы выбрали именно именно изменение времени почему? я вижу только такие решения:
1) либо это сделано для упрощения мат аппарата
2) либо это "намек" что КТП это лишь одна из версий того какой может быть вселенная , наша вселенная однонаправленная, но может быть вселенная с разными векторами времени
3) возможно есть иной вариант

можете подсказать какое решение верно или хотя бы куда копать, что бы уже поставить точку или если я не прав то в чем?

[amon]

hurt в сообщении #1706691 писал(а):

куда копать

Вы путаете две вещи - инвариантность к обращения времени и наличие "стрелы времени" в наблюдаемом мире. T-инвариантность это утверждение, что вероятности прямого и обратного процессов равны. Я выше приводил пример из механики. Это утверждение относится к микроскопическим процессам, включающим малое число частиц. К стати, время - не вектор, у него нет направления. "Стрела времени" появляется если рассматривать большие системы, содержащие большое количество "элементарных частиц". В этом случае кроме вероятности элементарного процесса надо учитывать насколько вероятно возникновение состояния с "переставленными" начальными и конечными состояниями всех составных частей большой системы. Изучение этого вопроса - предмет не КТП, а статистической физики, и строгого ответа на вопрос "почему наблюдаемый мир необратим, хотя почти все микроскопические уравнения обратимы во времени" пока не найдено. Обратимость во времени почти всех элементарных процессов, за исключением экзотических процессов типа распада нейтрального К-мезона, проверена экспериментально. Необратимость макроскопических процессов мы наблюдаем каждый день.

[Anton_Peplov]

Откуда берется стрела времени - действительно сложный вопрос, все еще не имеющий общепринятого ответа. На научно-популярном уровне он рассмотрен в книге: А. Чернин. Физика времени. Для чтения достаточно школьной программы. Для более продвинутого читателя есть такая рекомендация:

warlock66613 в сообщении #1508878 писал(а):

Есть обзорная книга на английском языке The physical basis of the direction of time за авторством Zeh. Там разбираются все стрелы времени в физике и их связь друг с другом. Для чтения крайне желательно знать 1) классическую и квантовую статистическую физику в минимальном объёме, 2) классическую электродинамику в объёме, примерно, Фейнмановских лекций по физике. Возможно, также потребуется предварительно отдельно познакомиться с декогеренцией, хотя в книге есть сверхкраткое представление — может быть его будет достаточно.

[hurt]

amon
спасибо кажется разобрался
1) как все-таки оказалось КТП изначально строилась на принципах симметрии
2) как писал уважаемый amon

amon в сообщении #1706737 писал(а):

К стати, время - не вектор, у него нет направления.

получается что так , в этом и была ошибка.
И да тогда все становится логичным :
КТП изначально строилась на принципах симметрии
Позже были обнаружены нарушения T-симметрии
а потом появилась теорема CPT
и так получается все сошлось.


Возникает еще один вопрос)

Если время можно представить как нечто расположенное на одной оси, при этом оно не имеет движения и вектора этого движения, получается что есть лишь движение во времени системы между состояниями системы, как я понял это движение так же не имеет вектора хотя можно менять его направление.
Тогда если вся Вселенная так симметрично даже в Т, почему происходит доминировании обычного вещества над антивеществом во Вселенной? И как я понимаю в большинстве случаев под антивеществом подразумеваются частицы с инвертированным C или P а не Т почему их по сравнению с обычным веществом мало?, но как я понимаю это уже риторические вопросы.

в целом большое спасибо за терпения всем, ребят, особенное спасибо Cos(x-pi/2) и amon

[amon]

hurt в сообщении #1706755 писал(а):

почему происходит доминировании обычного вещества над антивеществом во Вселенной?

Не волнуйтесь, этого никто не знает.

[Ende]

Неуместная в ПРР дискуссия выделена в тему «Стрела времени и квантовая механика».

[Ende]

Еще одна неуместная в ПРР дискуссия выделена в тему «Ведет ли обращение C, P и T к инверсии стрелы времени»