hurtЗапомним этот правильный ответ (вывод его у Вас требует исправлений, но пока на этом не задерживаюсь): под действием Р спин

не меняется, а импульс

заменяется на
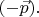
Это дальше будет важно в связи с понятием "спиральность" частицы. А то, что после Р шарик придётся нарисовать в другом месте пространства по отношению к неизменным осям

- это не будет дальше играть роли; вообще, параллельные переносы и повороты картинки с шариком как целого в 3-мерном пространстве не будут важны для обсуждения С, Р и Т.
В частности, вместо Р можно рассматривать отражение в какой-нибудь плоскости. Будет важно, что

и

при отражении ведут себя противоположным образом.
Например (можете проверить всё это, нарисовав себе картинки или представив себе зеркальное изображение движущихся и вращающихся шариков), если плоскость отражения выбрать параллельной к

то при таком отражении

не изменится; если же плоскость отражения параллельна
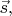
то

заменится на
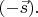
Если плоскость отражения перпендикулярна к

то

заменится на
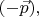
а если плоскость отражения перпендикулярна к
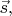
то

не изменится.
Все нелепые разговоры про якобы
в рамках нашей вселенной где время имеет один вектор движения, происходят компенсационные механизмы симметрии Т
давайте прекратим (если, конечно, Вы не хотите, чтобы эта тема отправилась в Пургаторий).
План пояснений у меня дальше такой: сначала рассмотрим на таком упрощёном языке (т.е. с классическими изображениями векторов

и
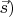
простейший конкретный пример реакции с элементарными частицами: превращение мезона

в антимюон

и мюонное нейтрино

Будем шаг за шагом применять к изображению этой реакции операции Р, С и Т и обсуждать, какие симметрии ("законы сохранения") выполняются, а какие нарушаются в этой реакции слабого взаимодействия.
Вот Вам очередная задачка для размышлений: рассматривая эту реакцию в системе покоя

изобразите себе, пожалуйста, зеркальную реакцию, т.е. такую реакцию, которая получилась бы после применения P к каждой частице; и попробуйте ответить на вопрос, почему такая зеркальная реакция в экспериментах никогда не наблюдается.
А я пока тоже подготовлю такой рисунок, для дальнейших пояснений.
-- 21.10.2025, 14:27 --уточните пожалуйста, а как это согласуется с подсказкой Cos(x-pi/2)
У меня речь шла о том, что инверсию шарика (и вообще любого тела в 3-мерном пространстве) можно представить как результат двух операций, выполненных в любом порядке (они коммутативны): 1) отражение в плоскости, перпендикулярной оси

и 2) поворот вокруг оси

на угол
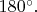
Любая точка тела с кординатами
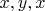
после указанного отражения переходит в точку с координатами
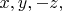
и затем получившаяся точка переходит после указанного поворота в точку с координатами
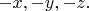
Это и есть инверсия.