Почему 3?

[Altenter]

Здравствуйте.
0. В 0-кубе 1 вершина и 0 ребер $1+0=3^0$.
1. В 1-кубе 2 вершины и одно ребро $2+1=3^1$.
2. В 2-кубе 4 вершины, 4 ребра и 1 грань $4+4+1=3^2$.
3. В 3-кубе 8 вершин, 12 ребер, 6 граней, 1 объем $8+12+6+1=3^3$.
И т.д.
Почему количество элементов в n-кубе равно именно $3^n$, а не какому-то другому числу?

[dgwuqtj]

Вам нужно это доказать для произвольного $n$? Грань в $n$-мерном кубе определяется тем, какое из множеств $\{0\}$, $[0, 1]$, $\{1\}$ может пробегать каждая координата. Всего $3^n$ и получается.

Каких-то более глубоких причин не знаю.

[Gagarin1968]

Altenter в сообщении #1704888 писал(а):

И т.д.

И т.д. не получается.
Уже в тессеракте 16 вершин, 32 ребра, 24 квадратных грани и 8 трёхмерных кубов (гиперграней гиперкуба, или в Вашей терминологии — объёмов). $16+32+24+8=80$. До $3^4$ не дотягивает.

[dgwuqtj]

Gagarin1968 в сообщении #1704892 писал(а):

До $3^4$ не дотягивает.

Ещё сам гиперкуб считается.

[Gagarin1968]

dgwuqtj в сообщении #1704893 писал(а):

Ещё сам гиперкуб считается

А, ну тогда возражение снимаю.

[Altenter]

dgwuqtj в сообщении #1704891 писал(а):

Вам нужно это доказать для произвольного $n$?

Положим да, и понять почему 3.

dgwuqtj в сообщении #1704891 писал(а):

Вам нужно это доказать для произвольного $n$? Грань в $n$-мерном кубе определяется тем, какое из множеств $\{0\}$, $[0, 1]$, $\{1\}$ может пробегать каждая координата. Всего $3^n$ и получается.

Каких-то более глубоких причин не знаю.

Спасибо, а можно об этом поподробнее? Что и куда пробегает? Что это у Вас за индексы в фигурных и квадратных скобках? И почему скобки разные?

[dgwuqtj]

Как обычно, $\{a\}$ обозначает множество из одного элемента $a$, $[0, 1]$ — отрезок с концами $0$ и $1$ на числовой прямой.

Например, в случае $n = 2$ был квадрат $[0, 1] \times [0, 1]$ (т.н. единичный квадрат). Вот все его грани:
$\{(0, 0)\} = \{0\} \times \{0\}$, $\{0\} \times [0, 1]$, $\{(0, 1)\} = \{0\} \times \{1\}$,
$[0, 1] \times \{0\}$, $[0, 1] \times [0, 1]$, $[0, 1] \times \{1\}$,
$\{(1, 0)\} = \{1\} \times \{0\}$, $\{1\} \times [0, 1]$, $\{(1, 1)\} = \{1\} \times \{1\}$.

Каждая грань — это произведение $n$ множеств, каждое из которых описывает, какие значения может принимать очередная координата. Для каждой координаты всего три варианта.

А вот если вам надо понять, почему все эти множества являются гранями и других граней нет, от вас понадобится определение грани. То есть «элемента» гиперкуба.

[Altenter]

dgwuqtj в сообщении #1704901 писал(а):

Как обычно, $\{a\}$ обозначает множество из одного элемента $a$, $[0, 1]$ — отрезок с концами $0$ и $1$ на числовой прямой.

Например, в случае $n = 2$ был квадрат $[0, 1] \times [0, 1]$ (т.н. единичный квадрат). Вот все его грани:
$\{(0, 0)\} = \{0\} \times \{0\}$, $\{0\} \times [0, 1]$, $\{(0, 1)\} = \{0\} \times \{1\}$,
$[0, 1] \times \{0\}$, $[0, 1] \times [0, 1]$, $[0, 1] \times \{1\}$,
$\{(1, 0)\} = \{1\} \times \{0\}$, $\{1\} \times [0, 1]$, $\{(1, 1)\} = \{1\} \times \{1\}$.

Каждая грань — это произведение $n$ множеств, каждое из которых описывает, какие значения может принимать очередная координата. Для каждой координаты всего три варианта.

А вот если вам надо понять, почему все эти множества являются гранями и других граней нет, от вас понадобится определение грани. То есть «элемента» гиперкуба.

Спасибо. Я в ступоре от этой нотации. Пробую понять.

[svv]

Хорошо. Вот Вам модификация этой системы обозначений. Поясню на примере трёхмерного куба. У него 0-мерные грани — вершины, 1-мерные — это рёбра, 2-мерные — это обычные грани, а 3-мерная — это сам куб.

Каждая грань кодируется словом из трёх символов. Возможные символы: 0 1 *
Вот несколько примеров граней: 010, 1*0, **1, ***.

Первый символ слова относится к координате $x$.
Если это 0, это значит, что у всех точек грани координата $x$ фиксирована и равна $0$.
Если это 1, у всех точек грани $x=1$.
А если это звёздочка *, то координата $x$ может пробегать значения от $0$ до $1$.

Аналогично, второй символ слова относится к координате $y$, а третий к координате $z$.

Что означает, например, **1 ? Что у точек этой грани $z=1$, а $x$ и $y$ принимают независимо произвольные значения от $0$ до $1$. Значит, это двумерная грань, а конкретно — верхняя грань куба (считая, что ось $Oz$ направлена вертикально вверх).

[gris]

мне показалось, что каждая грань однозначно определяется своей серединой. и можно посчитать, сколько середин имеется в конструкции. впрочем, у svv это наглядно видно, если звёздочку считать одной второй. и осталось посчитать количество середин, а значит и граней.
по индукции по размерности степень тройки достаточно наглядна и очевидна.

[TOTAL]

$\displaystyle (1+1+d)^n= \sum_{k=0}^n C_n^k\cdot 2^{n-k} \cdot d^k$, где $\displaystyle C_n^k\cdot 2^{n-k} $ -- число граней размерности k

[Altenter]

svv в сообщении #1704916 писал(а):

Хорошо. Вот Вам модификация этой системы обозначений. Поясню на примере трёхмерного куба. У него 0-мерные грани — вершины, 1-мерные — это рёбра, 2-мерные — это обычные грани, а 3-мерная — это сам куб.

Каждая грань кодируется словом из трёх символов. Возможные символы: 0 1 *
Вот несколько примеров граней: 010, 1*0, **1, ***.

Первый символ слова относится к координате $x$.
Если это 0, это значит, что у всех точек грани координата $x$ фиксирована и равна $0$.
Если это 1, у всех точек грани $x=1$.
А если это звёздочка *, то координата $x$ может пробегать значения от $0$ до $1$.

Аналогично, второй символ слова относится к координате $y$, а третий к координате $z$.

Что означает, например, **1 ? Что у точек этой грани $z=1$, а $x$ и $y$ принимают независимо произвольные значения от $0$ до $1$. Значит, это двумерная грань, а конкретно — верхняя грань куба (считая, что ось $Oz$ направлена вертикально вверх).

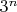
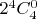
Спасибо, понял. Но не понял как получается отсюда общее число граней n-куба $ 3^n $. Вот на примере граней тессеракта, там ведь каждая грань кодируется уже словом из 4-х символов: есть двоичное слово ++++, вместо каждого плюсика может быть либо ноль, либо 1 и это мы закодируем все $2^4 C_4^0 $ 0-граней тессеракта. Затем посчитаем 1-грани. Они будут кодироваться словом вида +++*, где вместо + будет 0 или 1, А на месте звездочки величина будет пробегать значения от 0 до 1 и вот запись 000* - это 1-грань тессеракта из нуля в четвертое измерение $t$. 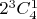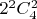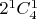Этих 1-граней в тессеракте будет $ 2^3C_4^1$, 2 грани записываются словом вида: ++** и их будет $2^2C_4^2$, 3-грани тессеракта записываются словом вида+*** и их будет $2^1C_4^1$ и единственная 4- грань запишется словом вида **** $2^0C_4^4$.

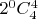
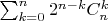
Итого граней тессеракта, если нигде не напортачил $\sum_{k=0}^n 2^{n-k}C_n^k$. Верно? Не соображу как показать, что это будет$ 3^n$.

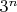
-- 08.10.2025, 12:33 --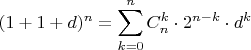

TOTAL в сообщении #1704950 писал(а):

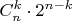
$\displaystyle (1+1+d)^n= \sum_{k=0}^n C_n^k\cdot 2^{n-k} \cdot d^k$, где $\displaystyle C_n^k\cdot 2^{n-k} $ -- число граней размерности k

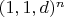
Спасибо! А что такое $d^k$??? Я обошелся без него при подсчете граней. И какое значение имеют $(1,1,d)^n$? В смысле что значат эти 1? Я так понимаю, что для любого n-куба количество его граней есть сумма этих неведомых единиц и d возведенных в степень $n$

[TOTAL]

Altenter в сообщении #1704957 писал(а):

А что такое $d^k$???

$k$ координат пробегают все значения из $(0,1)$. Остальные координаты застыли в одном из двух крайних положений. Вот такая грань и её размерность.

[dgwuqtj]

Altenter в сообщении #1704957 писал(а):

Не соображу как показать, что это будет$ 3^n$.

Бином Ньютона: $(a + b)^n = \sum_{k = 0}^n C_n^k a^k b^{n - k}$. Тут он применяется к $a = 1$ и $b = 2$.

[Altenter]

TOTAL в сообщении #1704960 писал(а):

Altenter в сообщении #1704957 писал(а):

А что такое $d^k$???

$k$ координат пробегают все значения из $(0,1)$. Остальные координаты застыли в одном из двух крайних положений. Вот такая грань и её размерность.

Спасибо. Ну, т.е. это дополнительный член для тех, кто не понимает по виду записи о какой грани идет речь? Вы кстати не ответили, что значат единицы в записи {1,1,d^k}^n или я не понял.

-- 08.10.2025, 13:03 --

dgwuqtj в сообщении #1704964 писал(а):

Altenter в сообщении #1704957 писал(а):

Не соображу как показать, что это будет$ 3^n$.

Бином Ньютона: $(a + b)^n = \sum_{k = 0}^n C_n^k a^k b^{n - k}$. Тут он применяется к $a = 1$ и $b = 2$.

Спасибо. Так а какой смысл у 1 и 2 (у $a,b$) в случае гиперкуба?