Еще раз про деление на ноль и значение синуса, достигающее 4

[EminentVictorians]

Mihr, еще в колесах можно делить на ноль. Но это, понятно, что не "на каждом шагу".

[Gastrit]

Mihr в сообщении #1704445 писал(а):

Равенства типа $\dfrac{1}{0}=\infty$ писать можно, но их обычно называют символическими равенствами

Это не совсем так. Точки сферы Римана (как и вещественной проективной прямой) при строгом определении - это пары $(z,w)$ со свойством $|z|+|w|\neq 0$, рассматриваемые с точностью до равенства вида $z_1w_2=z_2w_1$. То есть, попросту говоря - это дроби, в которых хотя бы что-то из числителя и знаменателя отлично от нуля. И топология там, в частности, вводится как раз под такие пары. Соответственно, бесконечная точка сферы Римана (или проективной прямой) - это именно и есть $1/0$, а вот $\infty$ - да, "условный символ".

Mihr в сообщении #1704445 писал(а):

Других примеров, как я понимаю, у вас нет?

Ну почему же, даже явно выше по ветке упомянуты. Линейные отношения и их спектральная теория, например. Скажем, вот такая матричнозначная функция:

$$R(z)=\begin{pmatrix}0&0\\ 0&-1/z\end{pmatrix}$$

рассматривается в указанной теории как резольвента некоторого конкретного линейного отношения, хотя действие любого из операторов $R(z)$ (при $z\neq 0$) на базисный вектор $e_1$ есть "умножение на нуль", и потому "обращать эти операторы нельзя".

Конечно, кто с такими вещами непосредственно не сталкивался (а содержательно они рассматриваются скорее в бесконечномерном случае, чем в приведённом мной простеньком двумерном), тому это тоже может показаться бессмысленным вывихом ума. Но вот, скажем, самосопряжённые расширения симметрических дифференциальных операторов (совершенно однозначных) описываются именно в терминах симметрических отношений между граничными значениями, и ничего тут особо не поделать.

[ozheredov]

Промежуточный итог:

Альты - 1
Mihr - 0

[Mihr]

Gastrit, мне понятно отнюдь не всё, что вы говорите, но у меня не проходит ощущение, что вы пользуетесь неким собственным языком и называете "делением на ноль" то, что остальные люди так не называют. Я сам могу привести куда более простой пример. Скажем, запись уравнения прямой в виде

$$\dfrac{x-6}{3}=\dfrac{y+1}{0}=\dfrac{z-4}{-2}$$

означает всего-навсего, что направляющий вектор этой прямой $\vec{l}=(3;0;-2)$, а вовсе не то, что в процессе решении какой-то задачи, связанной с этой прямой, нам придётся выполнять деление на ноль. Но вполне возможно, что кто-нибудь и воскликнет: смотрите, а ведь здесь делят на ноль!
Или несколько более сложный пример: при перемножении квадратных матриц их определители перемножаются, значит, вырожденная матрица в принципе не может иметь обратной. Однако можно построить псевдообратную матрицу и заявить: смотрите, мы разделили на ноль!
Но это лишь жаргон, и к реальному делению на ноль всё это отношения не имеет.
Ваши примеры мне представляются довольно специфичными, и тезис о том, что в математике "деление на ноль встречается чуть ли не на каждом шагу" они на мой взгляд всё же никак не подтверждают. Во всяком случае, операции деления на ноль, понимаемый именно как нейтральный относительно сложения элемент кольца $\mathbb{Z}$ (либо поля $\mathbb{Q}$, $\mathbb{R}$ или $\mathbb{C}$), а не в каком-то ином смысле, я всё же не увидел (возможно, мне это просто не дано, не знаю ). А речь ведь шла, как я понимаю, именно о таком нуле.
Пример с композицией дробно-линейных отображений - это снова отсылка к расширенной комплексной плоскости. Чего-то существенно иного я в этом примере не вижу.

(ozheredov)

ozheredov, спасибо. Когда мне вновь потребуются услуги рефери, я буду знать, кому писать ЛС

[EUgeneUS]

Mihr в сообщении #1704477 писал(а):

Во всяком случае, операции деления на ноль, понимаемый именно как на нейтральный относительно сложения элемент кольца $\mathbb{Z}$ (либо поля $\mathbb{Q}$, $\mathbb{R}$ или $\mathbb{C}$), а не в каком-то ином смысле, я всё же не увидел .... А речь ведь шла, как я понимаю, именно о таком нуле.

Именно так, и никак иначе.

ozheredov в сообщении #1704453 писал(а):

Альты - 1

Вы даже команду не смогли правильно назвать.
Gastrit - никакой не "альт". Какие-то остаточные знания у него имеются, видимо.
Просто голову морочит, в чём наблатыкался в уютной жежешечке, и решил тут силы попробовать

-- 04.10.2025, 21:46 --

ИМХО, нужно сдать в поликлинику для опытов отправить в поля искать делители нуля.
Но это уже администрации решать, конечно.

[Gastrit]

Mihr в сообщении #1704477 писал(а):

операции деления на ноль, понимаемый именно как на нейтральный относительно сложения элемент кольца $\mathbb{Z}$ (либо поля $\mathbb{Q}$, $\mathbb{R}$ или $\mathbb{C}$), а не в каком-то ином смысле, я всё же не увидел

Вы подменяете предмет обсуждения. Я сразу сказал, что никакого "единого общего решения проблемы деления на нуль" нет и не может быть. Могут быть различные способы придания смысла соответствующим выражениям в различных конкретных ситуациях. Друг с другом, вообще говоря, не совместимые.

В проективной геометрии и комплексном анализе придаётся смысл выражениям $a/0$ при $a\neq 0$ - но это требует выхода за рамки первоначального множества объектов. При этом остаются принципиально бессмысленными отношения вида $0/0$. Это - факт номер один.

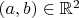
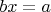
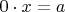
Рассмотрение деления как многозначной функции, сопоставляющей всякой паре $(a,b)\in\mathbb R^2$ решение уравнения $bx=a$, придаёт смысл именно выражению $0/0$ (за которым теперь может скрываться любое $x\in\mathbb R$ как решение уравнения $0\cdot x=0$), но делает принципиально бессмысленными отношения вида $a/0$ при $a\neq 0$ (ввиду неразрешимости уравнения $0\cdot x=a$). Это - факт номер два.

В общем, каждая конкретная ситуация тут требует своего подхода и даёт свои результаты. Вот о чём шла речь. В то время как мой оппонент с учебником для 2-го класса наперевес годами верещал - "нет! никак! никогда! нельзя делить на нуль! ни в каком смысле нельзя! как суть конкретной задачи ни поясняй!".

Ну да, задолбал он меня своим агрессивным невежеством, и своим "на каждом шагу" я в некотором смысле палку, конечно, перегнул. Не на каждом. Но в целом ряде областей это, тем не менее, в той или иной форме делается. Либо в смысле проективных пространств. Либо в смысле формального обращения ("выворачивание графика") линейных операций с нетривиальным ядром (что на выходе даёт многозначные не всюду определённые "функции", то есть вот те самые линейные отношения). И никого из специалистов в соответствующих тематиках это всё не смущает. Против такой констатации возражения имеются?

-- 04.10.2025, 22:43 --

EUgeneUS в сообщении #1704478 писал(а):

нужно сдать в поликлинику для опытов отправить в поля искать делители нуля.
Но это уже администрации решать, конечно.

Да, конечно. Однако смею заметить, что на Ваши прежние обвинения меня в невежестве мной выше был дан предметный комментарий:

Gastrit в сообщении #1704260 писал(а):

EUgeneUS в сообщении #1704256 писал(а):

"Курс дифференциального и интегрального исчисления" Фихтенгольца и раскрытие неопределённости вида 0/0 к этому отношения не имеют.

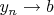
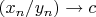
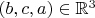
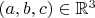
Имеют, и самое прямое. Неопределённости связаны в том числе с тем фактом, что предел произведения сходящихся последовательностей есть произведение пределов сомножителей. И пределы эти - именно числа. То есть в случае $x_n\to a$, $y_n\to b$ и $(x_n/y_n)\to c$ точка $(b,c,a)\in\mathbb R^3$ лежит на графике умножения, а точка $(a,b,c)\in\mathbb R^3$ - на графике "честного" (то есть многозначного) деления. Факт этой многозначности по существу пресловутую неопределённость и создаёт.

Это замечание Вами никак не прокомментировано. Можно поинтересоваться, почему? Возразить нечего, а признать, что недопоняли позицию оппонента, не хочется?

[Mihr]

Gastrit в сообщении #1704486 писал(а):

Вы подменяете предмет обсуждения

Да нет, мы просто говорим о разных вещах, очевидно. Я изначально отвечал вообще не вам и именно по поводу деления на число ноль. "Различные способы придания смысла" я ни разу не имел в виду. Что и подчеркнул в предыдущем посте.
Давайте уже замнём для ясности. Надоело, честно говоря.

-- 04.10.2025, 22:51 --

Gastrit в сообщении #1704486 писал(а):

Против такой констатации возражения имеются?

Нет.

[Gastrit]

Mihr в сообщении #1704487 писал(а):

Я изначально отвечал вообще не вам

Простите, но Вы отвечали в теме, начатой словами "встретился с неким товарищем (вроде бы даже выпускником мехмата МГУ), который не раз и не два утверждал, что деление на ноль не только возможно, но и постоянно происходит". То есть сказанное Вами автоматически представляет собой оценку точки зрения этого "некоего товарища". А эта точка зрения состоит именно в "различных способах придания смысла".

Вы констатируете, что эта точка зрения изначально была понята Вами - с чужих слов - неправильно, и входить в её разбор по существу Вы теперь (получив дополнительные разъяснения) не намерены? Если так, то я не возражаю.

Mihr в сообщении #1704487 писал(а):

Gastrit в сообщении #1704486 писал(а):

Против такой констатации возражения имеются?

Нет.

Большое спасибо.

[Mihr]

(Gastrit)

Gastrit в сообщении #1704488 писал(а):

сказанное Вами автоматически представляет собой оценку точки зрения этого "некоего товарища"

Нет. Сказанное мной относится именно к тому тексту, который я прочитал. Насколько точно были переданы ваши слова, я не знаю, конечно.

Если кто-нибудь сообщает: мне рассказали так-то и так-то, это верно или нет? - я в таких случаях просто отвечаю "верно" или "неверно" (если могу ответить). Не пытаюсь при этом выяснить, насколько точно переданы чьи-то слова. Просто отвечаю на вопрос.
Вы поступаете иначе? Говорите: возможно, имелось в виду то-то, а может, и вот то-то, а может, ещё что-то третье? Если вы отвечаете именно так, это ваше право, конечно. Но едва ли стоит требовать подобного подхода и от всех остальных.

[ozheredov]

EminentVictorians в сообщении #1704447 писал(а):

еще в колесах можно делить на ноль

Можно делить на ноль, закинувшись колёсами

[EUgeneUS]

Gastrit в сообщении #1704486 писал(а):

Однако смею заметить, что на Ваши прежние обвинения меня в невежестве мной выше был дан предметный комментарий:

Смею заметить, что
а) я Вас не обвинял
б) не в невежестве.

Вы опять врёте и передергиваете.

Ваше поведение было охарактеризовано, как шулерство и подмена понятий. Никаких обвинений в невежестве.

EUgeneUS в сообщении #1704256 писал(а):

с делением на ноль - это шулерство и подмена понятий со стороны Вашего оппонента.

Gastrit в сообщении #1704486 писал(а):

Это замечание Вами никак не прокомментировано. Можно поинтересоваться, почему?

Поинтересоваться можно.
Ваши подобные вопросы возникают по причине того, что Вы не читаете внимательно что Вам пишут.
Было сказано:

EUgeneUS в сообщении #1704256 писал(а):

А более подробно тут смысла говорить нет.

С чего Вы решили, что на Ваши закидоны, манипуляции, шулерство и подмену понятий будут дадены какие-то развернутые комментарии?

Gastrit в сообщении #1704486 писал(а):

Возразить нечего, а признать, что недопоняли позицию оппонента, не хочется?

Это уже переход на личности.

[Ende]

Настоятельно прошу всех участников умерить эмоции и прекратить обсуждать друг друга.

[Gastrit]

EUgeneUS в сообщении #1704517 писал(а):

Вы опять врёте и передергиваете. Ваше поведение было охарактеризовано, как шулерство и подмена понятий. Никаких обвинений в невежестве.

Обвинения во "вранье" и "передёргивании" - штука сама по себе милая. Однако выше Вами было сказано ещё и вот это:

EUgeneUS в сообщении #1704478 писал(а):

Какие-то остаточные знания у него имеются, видимо.

А вот это уже граничит с обвинением именно в невежестве.

Между тем как если Вы автоматически не видите, что неопределённости из теории пределов связаны с теоремой о пределе произведения (на что я и указал в первом же своём комментарии), то "остаточными" следует считать скорее как раз Ваши знания, а не мои.

Я вижу, на каком уровне находятся многие здешние обсуждения, и потому могу понять Ваши чувства при виде "свежего" пользователя, которому притом ещё до его появления сделали соответствующую рекламу. Однако это не повод уклоняться от ответов по существу.

[Ende]

Вопрос о невозможности деления на ноль и о смысле разных операций, отчасти похожих на деление на ноль, обсуждался на форуме неоднократно. В этой теме, кажется, тоже сказано примерно все, что можно сказать по существу вопроса. Переругивание вокруг знаний и намерений отдельных участников не нужно вообще, и тем более в математическом разделе. Тема закрыта.