Именно так. Есть функция

, с графиком, составленным из всевозможных точек вида
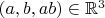
. И есть обратное к ней отношение с графиком, составленным из точек вида
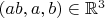
. Это отношение не является графиком функции ввиду неоднозначности определения значения

парой
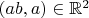
в случае
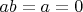
, и потому в школе такой случай механически отбрасывают (разумеется, парить младшеклассникам мозги многозначными отображениями бессмысленно, если не прямо вредно). Но это никак не отменяет того, что формальное обращение умножения даёт именно многозначную (в одной точке) функцию.
Почему в одной точке? Уможение это (однозначная) функция вида

. Обратной к этой функции будет многозначная функция вида

. А у вас написана какая-то не особо понятная фраза про " неоднозначность определения значения

парой
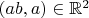
", как будто под обратной функцией (которая многозначная) вы почему-то считаете такого вида:

, а не

как надо бы.
Фраза "деление - это функция, обратная умножению" - это не более, чем фигура речи. Строго говоря, деление (как функция вида
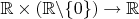
) не является функцией, обратной к умножению (функции вида
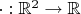
).
Неоднозначность (многозначной) функции, обратной к умножению (то есть функции вида
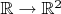
) будет в любой точке, а не только в одной.
У деления (функции вида
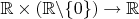
) никакой неоднозначности нету, она - нормальная однозначная функция.
Вы, по-моему, хотите рассматривать функцию, которая по произведению и первому множителю выдает второй. Так можно, и она действительно будет многозначной в единственной точке

. Но называть её "формальным обращением умножения" не стоит.