И тогда для черной дыры это:
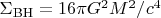
Для вселенной:
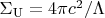
Вы показали
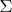
для ЧД и для вселенной, это частные случаи, так? Возможно по-вашему из этих двух частных случаев все сами должны были понять как должен выглядеть общий случай, но можете вы показать как должен выглядеть общий случай?
И причём тут ЧД и "вселенная" к тёмной материи? Вы буквально сразу после этого ниже по тексту начинаете говорить о тёмной материи, но зачем-то приводит пример вычисления
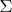
для ЧД и "вселенной", вместо того что надо.
А что ещё может ваша теорию кроме якобы объяснения тёмной материи?