Квантовая физика атома водорода без интерпретаций

[amon]

Cos(x-pi/2) в сообщении #1702435 писал(а):

Без "портянки", хотя бы кратенькой, всё-таки непонятно, как эта волновая функция оказалась точным решением уравнения Шрёдингера $i\dot{\Psi}=H\Psi.$

Для Вас - с превеликим удовольствием. Вы написали столько хороших текстов, что грех отказываться. Чтобы народ не пугать, спрячу под спойлер.

(Оффтоп)

Перепишем нашу систему в представлении Фока-Баргмана. Введем переменные $\theta$ -- грассманово комплексное, а $z$ -- обычное комплексное число. $a^+=z\,,a=\frac{\partial}{\partial z}\,,C^+= \theta\,,C=\frac{\partial}{\partial \theta}.$ Гамильтониан перепишется так:

$$\begin{align*} H&=\varepsilon C^+ C+\omega a^+ a+g\left(a^+ C+ C^+ a\right) + \alpha\left(E\left(t\right)C^+ + E^*(t)C\right)\\ &=\varepsilon\theta\frac{\partial }{\partial \theta} + \omega z\frac{\partial }{\partial z}+g\left(z\frac{\partial }{\partial \theta}+\theta\frac{\partial }{\partial z}\right) + \alpha \left(E(t)\theta+E^*(t)\frac{\partial }{\partial \theta}\right). \end{align*}$$

Базисные состояния (состояния с ненулевыми матричными элементами гамильтониана)

$$\begin{align*} |0,0\rangle&=1\;\text{определение вакуума в Фоке-Баргмане}\\ |1,0\rangle&=C^+|0,0\rangle=\theta\\ |0,1\rangle&=a^+|0,0\rangle=z.\\ \end{align*}$$

Фокус тут в том, что я считаю, что классическое поле отличимо от моды резонатора, например, по поляризации. Если начальное состояние - вакуум, то можно подобрать параметры возбуждающего импульса так, что состояние $|1,1\rangle$ возникнуть не может. Система двухуровневая, фотон излучается только при переходе из возбужденного в основное состояние, внешнее поле я выключаю когда фотон еще не излучился, поэтому в резонаторе остается единственный фотон.
Волновая функция

$$\Psi=c_1(t)|0,0\rangle+c_\theta(t)|1,0\rangle + c_z(t)|0,1\rangle.$$

Матрица гамильтониана в этом базисе

$$H=\begin{pmatrix} 0&-\alpha E^*(t) &0\\ -\alpha E(t) & \varepsilon & g\\ 0 & g & \omega \end{pmatrix} $$

Уравнения Шредингера получается умножением этой матрицы на столбец коэффициентов $c_i(t)$:

$$\begin{align} i\dot c_1&=-\alpha E^*(t)c_\theta\\ i\dot c_\theta&= -\alpha E(t)c_1+\varepsilon c_\theta +g c_z\\ i\dot c_z&=g c_\theta + \omega c_z. \end{align}$$

Выбором единиц положим $g=1.$ Введем новые переменные

$$\begin{align*} c_\theta&=e^{-i\varepsilon t}c_\theta\\ c_z&=e^{-i\omega t}c_z\\ \end{align*}$$

и будем считать, что $E(t)=\alpha E(t)e^{i\omega_0 t},$ где $E$ в правой части -- финитная вещественная медленно меняющаяся функция. В точном резонансе ($\omega=\omega_0=\varepsilon$) получится

$$\begin{align} i\dot c_1&=- E(t)c_\theta \label{с1}\\ i\dot c_\theta&= - E(t)c_1 + c_z\\ i\dot c_z&= c_\theta. \end{align}$$

Данные уравнения описывает двухуровневый атом в резонаторе бесконечной добротности, в котором с помощью шаманского бубна включили и выключили внешнее классическое поле. Тем не менее, они качественно позволяют понять, что происходит в реальной системе при возбуждении коротким импульсом. Для прямоугольного импульса длиной $\tau$ ($E(t)=E(\theta(t)-\theta(\tau-t))$) все решается аналитически, поскольку при $t<\tau$ коэфффициенты уравнения постоянны.
На графике приведено численное решение этой системы для огибающей в виде одного периода функции

$$E_0\cos^2\left( \frac{\pi(t-t_0)}{2\tau}\right),$$

где $t_0$ - положение максимума "импульса", а $\tau$ - его полуширина, поскольку для прямоугольного импульса уравнение с разрывной производной численно решается хреново.

[realeugene]

amon в сообщении #1702441 писал(а):

внешнее поле я выключаю когда фотон еще не излучился, поэтому в резонаторе остается единственный фотон.

Но это уже приближение: если возможность излучения включена с нуля, то очевидно, что в точном решении будет пусть и очень быстро убывающий, но бесконечный ряд по количеству фотонов в резонаторе.

При параметрах, при которых нарисован график, какие-то единицы процентов придут к состоянию $|1,1\rangle$.

-- 20.09.2025, 12:12 --

amon в сообщении #1702441 писал(а):

Если начальное состояние - вакуум, то можно подобрать параметры возбуждающего импульса так, что состояние $|1,1\rangle$ возникнуть не может.

Как, если только не в пределе очень короткого импульса? В гамильтониане член, отвечающий за возбуждение атома классическим полем, не зависит от фотонов.

[Cos(x-pi/2)]

amon
Спасибо большое!

Систему уравнений

$$\begin{align} i\dot c_1&=-\alpha E^*(t)c_\theta\\ i\dot c_\theta&= -\alpha E(t)c_1+\varepsilon c_\theta +g c_z\\ i\dot c_z&=g c_\theta + \omega c_z. \end{align}$$

я получил сразу (просто руками полагая равными нулю амплитуды всех состояний $|0,m\rangle$ c $m>1$ и $|1,n\rangle$ c $n>0,$ а иначе там конца и края не видно в цепочке уравнений). И решил эту систему пока в элементарном случае: при отсутствие источника, $E(t)=0,$ с условием точного резонанса $\omega=\varepsilon$ :) При этих условиях нашлись три стационарных состояния системы:

$|0,0\rangle$ с энeргией $0,$

$\frac{1}{\sqrt{2}}(|1,0\rangle +|0,1\rangle)$ с энергией $\varepsilon + g,$

$\frac{1}{\sqrt{2}}(|1,0\rangle - |0,1\rangle)$ с энергией $\varepsilon - g.$

При $E(t)\neq 0$ задача кажется похожей на обычную в механике задачу о двух связанных осцилляторах в присутствии внешней силы, действующей на конечном промежутке времени; сначала так и попробую дорешать. (Увы, для активного владения техникой Фока-Баргмана я пока твердоват, опыта такого не имею; но ещё надеюсь освоить, пытаюсь всему понемногу учиться, как "вечный студент" :)

Ещё раз спасибо Вам большое!

[realeugene]

Cos(x-pi/2) в сообщении #1702490 писал(а):

Если это верно, то основное состояние системы это не "вакуум" $|0,0\rangle$ (как было бы при отсутствии связи атома с резонатором, т.е. при $g=0),$ а суперпозиция состояний $|1,0\rangle$ и $|0,1\rangle$ (с минусом, если $g>0$ или с плюсом, если $g<0).$

А обязательное совпадение частот не означает, что эти числа равны по модулю, и одна из этих энергий нуль, а вторая положительная?

[Cos(x-pi/2)]

realeugene
А, да, спасибо. Это я погорячился спросонья. Сейчас отредактирую - уберу все слова про основное состояние. Разумно предполагать, что энергия возбуждения атома $\varepsilon>0$ - не малая величина, а $g$ - по сравнению с ней это малая по абсолютной величине "константа связи" атома с резонатором, и тогда $\varepsilon\pm g>0.$

[realeugene]

Cos(x-pi/2)
Точно, и я тоже не посмотрел на исходную систему уравнений, подумав на $g$ что это $\omega$.

[Ende]

Все предыдущие сообщения в этой теме - копии сообщений из темы «Ветвление миров в многомировой интерпретации кв. механики». Копии сделаны для желающих обсудить физику атома водорода, не вдаваясь в интерпретации квантовой механики.

Оригиналы всех сообщений сохраняются в теме «Ветвление миров в многомировой интерпретации кв. механики», продолжать обсуждение интерпретаций можно там.

[Cos(x-pi/2)]

Насчёт похожести на обычную задачу об осцилляторах под действием внешней силы $F(t)$ я ошибся.

(Оффтоп)

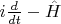
Схематично дело выглядит вот как. Допустим, линейный "оператор уравнения движения" $\hat{K}$ означает $i\frac{d}{dt}-\hat{H}$ без внешней силы в задаче, предложенной выше уважаемым amon. В задаче об осцилляторах оператор $\hat{K}$ будет отчасти аналогичен, c $\frac{d^2}{dt^2}$ вместо $i\frac{d}{dt}.$

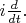
В присутствии внешней силы $F(t)$ уравнение движения для колебаний осцилляторов $\Psi(t)$ это

$$\hat{K}\Psi=F$$

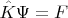
Его решение при нулевых начальных условиях можно выразить через запаздывающую функцию Грина:

$$\Psi(t)=(G(t-t'),F(t'))$$

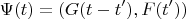
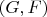
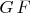
где $(G,F)$ означает интеграл от $G\,F$ по $t'.$

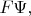
Но в задаче про атом правая часть уравнения движения это не $F,$ а $F\Psi,$ и таким путём получим не готовое решение $\Psi,$ а интегральное уравнение:

$$\Psi=(G,F\Psi)\,.$$

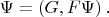
Так что, в общем случае нужно решать уравнение для $\Psi(t)$ численно.

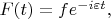
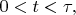
Согласно пояснению amon, в частном случае - с внешней силой в виде импульса длительностью $\tau$ с П-образной огибающей, т.е. $F(t)=fe^{-i\varepsilon t},$ где $f$ это не равная нулю постоянная при $0<t<\tau,$ а вне этого промежутка времени $f$ равна нулю, - решение легко выводится аналитически. Начальное условие при $t=0$ у нас такое - атом не возбуждён и поле в резонаторе не возбуждено (ноль фотонов):

$$|\Psi(0)\rangle=1\cdot |0,0\rangle +0\cdot |1,0\rangle+0\cdot |0,1\rangle$$

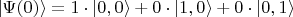
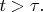
Решение $|\Psi(t)\rangle$ при $t=\tau$ даёт нам новые значения коэффициентов в такого рода суперпозиции базисных состояний. 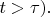Эти новые значения коэффициентов служат новым начальным условием для решения $|\Psi(t)\rangle$ при $t>\tau.$ В общем виде решение при $t>\tau$ нам уже известно: это суперпозиция упомянутых выше трёх стационарных состояний (стационарных, потому что внешняя сила, возбуждающая атом, равна нулю при $t>\tau).$ Квадраты модулей коэффициентов такого решения при базисных векторах состояния дают нам вероятности; ниже на рисунке они у меня обозначены так:

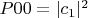
$P00=|c_1|^2$ - вероятность обнаружить систему в состоянии $|0,0\rangle,$ т.е. атом не возбуждён и фотон не рождён;

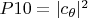
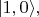
$P10=|c_{\theta}|^2$ - вероятность состояния $|1,0\rangle,$ т.е. атом возбуждён, но фотон ещё не рождён (или уже поглощён атомом, если был рождён атомом раньше);

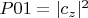
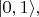
$P01=|c_z|^2$ - вероятность состояния $|0,1\rangle,$ т.е. атом вернулся в невозбуждённое состяние, родив $1$ фотон.

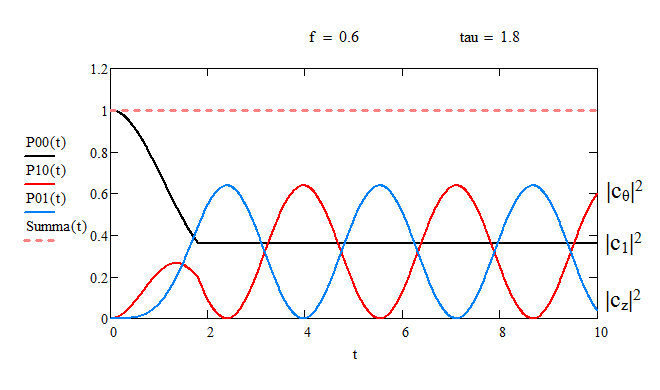
Вывод формул не пишу (можно будет написать, если возникнут сомнения в правильности, или если у кого-то не получится вывести самостоятельно), а привожу графики со значениями параметров $f$ и $\tau,$ которые в этом примере я выбрал так, чтобы получился результат, качественно напоминающий показанный уважаемым amon результат для случая с гладким возбуждающим импульсом.



Заодно вот пара рисунков с другими значениями параметров: здесь длительность импульса уменьшена, а возбуждающа сила увеличена так, что получаются примерно прежние вероятности; здесь по сравнению с предыдущим случаем возбуждающая сила уменьшена.

Такие модельные примеры показывают, во-первых, что внешним полем можно создавать суперпозиции стационарных состояний системы "атом + поле". Во-вторых, видно, как со временем возбуждённый атом переходит (в смысле изменяются коэффициенты суперпозиции, и тем самым изменяются вероятности состояний) в невозбуждённое состояние за счёт спонтанного рождения фотона. Фотон остаётся внутри резонатора, и со временем атом его вновь поглощает. И всё повторяется; это осцилляции Раби с частотой $2g$ при точном резонансе $\omega=\varepsilon$ и $f=0.$ В резонаторе с бесконечной добротностью осцилляции не затухают.

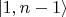
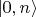
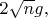
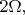
Можно аналогично рассмотреть переходы между состояниями $|1,n-1\rangle$ и $|0,n\rangle$ при $n>1.$ Частота осцилляций вероятностей при $f=0$ получается, если не ошибся, равной $2\sqrt{n}g,$ а при не точном резонансе $2\Omega,$ где

$$\Omega=\sqrt{\frac{(\varepsilon-\omega)^2}{4}+ng^2}$$

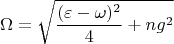
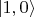
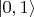
Далее хорошо бы попытаться разобрать модель с переходом из $|1,0\rangle$ в $|0,1\rangle$ уже не в резонаторе с единственной резонансной модой поля, а в "ящике" сколь угодно большого объёма $V.$ Моды поля в таком случае имеют "густой" спектр собственных частот, многие из них оказываются почти в резонансе с частотой атомного перехода $\varepsilon.$ Можно предположить, что в этой модели получим уже не осцилляции, а релаксацию атома на нижний уровень энергии, и, может быть, удастся подобраться к оценке времени жизни возбуждённого состояния. (Такой, вроде, возможен план самообразования в азах КТП. Пока без эффектов типа рождения и аннигиляции пар частица-античастица, лэмбовского сдвига уровней, расходимостей и перенормировок. Мда... мечты, мечты.)

[Alex-Yu]

epros в сообщении #1703453 писал(а):

Я вижу, что в состоянии с неопределённой энергией осциллируют плотности зарядов и токов, что означает неизбежное взаимодействие с электромагнитным полем, так что электрон в этом состоянии вечно оставаться не может.

Если осциллирующей плотности заряда и тока нет (например, в p-состоянии водорода без какой-либо примеси), то тоже излучение есть (если поле квантовое). Так что это все ни о чем, очередная попытка натянуть сову на глобус (кванты на классику или наоборот, это кому уж как больше нравится).

[amon]

Cos(x-pi/2) в сообщении #1703661 писал(а):

Далее хорошо бы попытаться разобрать модель с переходом из $|1,0\rangle$ в $|0,1\rangle$ уже не в резонаторе с единственной резонансной модой поля, а в "ящике" сколь угодно большого объёма $V.$ Моды поля в таком случае имеют "густой" спектр собственных частот, многие из них оказываются почти в резонансе с частотой атомного перехода $\varepsilon.$ Можно предположить, что в этой модели получим уже не осцилляции, а релаксацию атома на нижний уровень энергии, и, может быть, удастся подобраться к оценке времени жизни возбуждённого состояния.

Там так ловко не получится. Время жизни сосчитать можно, а лэмбовский сдвиг (сдвиг уровня энергии атома за счет взаимодействия с полем) - нет. Там возникает знаменитая ультрофиолетовая расходимость. Будет время - попробую написать.

[Alex-Yu]

Cos(x-pi/2) в сообщении #1703661 писал(а):

Так что, в общем случае нужно решать уравнение для $\Psi(t)$ численно.

Задача о квантовом осцилляторе, возбуждаемом классической силой решается аналитически. Получается осциллятор в когерентном (глауберговском) состоянии. Причем решается точно и в элементарных функциях. Во всяком случае если начальное состояние этого осциллятора основное ("вакуум"). Если начальное состояние не основное, то на вскидку что-то не соображу так уж сразу.

P.S. Пожалуй, можно и при неосновном начальном. Во всяком случае в гайзенберговском представлении вообще все равно, какое начальное состояние. Уравнения Гайзенберга от состояния не зависят вообще. И они в этой задаче решаются.

[Cos(x-pi/2)]

Alex-Yu в сообщении #1704235 писал(а):

Задача о квантовом осцилляторе, возбуждаемом классической силой решается аналитически. Получается осциллятор в когерентном (глауберговском) состоянии.

Задача о квантовом осцилляторе - да, решается так, как Вы сказали.

Ну а здесь другой пример: ищется решение для взаимодействующих ферми- и бозе- подсистем, притом такое, что актуальных базисных состояний всей системы будет всего три. Для бозе-подсистемы два - с нулём квантов и с одним; это не когерентное состояние осциллятора.

[pppppppo_98]

Cos(x-pi/2) в сообщении #1703468 писал(а):

Вот и задумался теперь, а известен ли вообще какой-то физически осмысленный способ определить "среднее время жизни" частицы в смеси нестабильных частиц, различающихся временем жизни? (Гуглежом подходящего ответа не нашёл; может быть, плохо искал... или какой-то заскок у меня (увы, такое бывает)).

вы не можете найти ответа, потому что его нет в природе, ибо нет никакого физического или математического смысла в сумме экспонет... В атомной промышленности эта задача стоит со времен первых атомных реакторов. ОЯТ - это смесь изотопов с разными рериодами полураспада, и вот когда строят график активности ОЯТ в логарифмическом масштабе - то там как и положено - куски прямых (в сотвествии с иерархиейвремен распадов отдельных компонентов оят). От этого графика отталкиваются стратегии переработки и зазоронения оят... во всей этой тематике с пуассново/экспотенциальными рапределениями ваша формула с суммой обратных времен возникает когда есть ветвление проуессов распадов с разной вероятностью и разными временами на разных ветках (можно вывести аналитически временную константу общей эволюции распадающегося материала)

[realeugene]

amon в сообщении #1703510 писал(а):

$$H=\varepsilon C^+ C+\omega a^+ a+g\left(a^+ C+ C^+ a\right) + \alpha\left(E\left(t\right)C^+ + E^*(t)C\right).$$

Четвёртый член отвечает за запуск колебаний. После отключения внешнего поля он дальше нуль. Первые два члена отвечают за независимое вращение квантовых фаз возбуждённых состояний атома и поля. При этом возбуждённые состояния сами по себе являются стационарными и сохраняются этими членами сколь угодно долго без перехода в ортогональное состояние. За переход отвечает только член $g\left(a^+ C+ C^+ a\right)$. Когда атом возбуждён и фотона нет, система находится в чистом состоянии $|1,0\rangle$. И первое слагаемое $a^+ C$ отображает это и только это состояние в $|0,1\rangle$, то есть

$$a^+ C\propto |0,1\rangle \langle 1,0|$$

Это и означает мгновенный переход атома из возбуждённого состояния в невозбуждённое с одновременным появлением фотона. При этом наличие в суперпозиции состояния $|0,0\rangle$ вообще ни на что не влияет, так как после отключения внешнего поля оно сидит в ядре гамильтониана. Я ещё ничего не забыл?

[realeugene]

realeugene в сообщении #1704356 писал(а):

то есть

$$a^+ C\propto |0,1\rangle \langle 1,0|$$

Это и означает мгновенный переход атома из возбуждённого состояния в невозбуждённое с одновременным появлением фотона.

А самое тут занятное, что чтобы начала при этом уменьшаться вероятность нахождения в состоянии без фотона $|1,0\rangle$, необходима в суперпозиции ненулевая примесь состояния $|0,1\rangle$ и воздействующий на неё член гамильтониана $C^+a\propto |1,0\rangle \langle 0,1|$, отвечающий за распад состояния с фотоном обратно в состояние без фотона и с возбуждённым атомом. В момент пока фотона совсем нет модуль амплитуды растёт в первом порядке малости по времени, а вероятность - только во втором.

А как уменьшается амплитуда вероятности атому находиться в возбуждённом состоянии в КЭД с бесконечным пространством, если фотон уже улетел?