Ну, ок. Сконструировали крокодила. И чему в эмпирике оно соответствует?
Пока не знаю. Если в качестве пробной механической частицы рассмотреть (само)вращающийся Меркурий, который еще вращается вокруг (само)вращающегося Солнца, то, наверное, вот такие два вектора
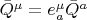
и
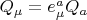
будут описывать динамику двумерной плоскости (само)вращения Меркурия и определят вклад в правую часть уравнения мировой линии Меркурия за счёт взаимодействия с тетрадной связностью
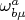
обусловленной (само)вращающимся Солнцем

звыняюсь... а что такое заряд в ваше терминологии? Скаляр, тензор? как он преобразуется при калибровочных преобразованиях...
В точке

пространства-времени рассмотрим слой тетрадного расслоения (который представляет собой векторное пространство), в котором введём координаты

, тогда тетрадная связность в точке
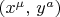
имеет следующие компоненты:
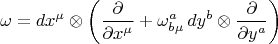
Эти самые "заряды" о которых Вы спрашиваете это векторы в этом векторном пространстве:
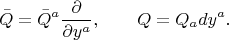
Если в том векторном пространстве сделать преобразование тетрадных координат
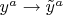
, то компоненты тетрадной связности и зарядовых векторов преобразуются так:
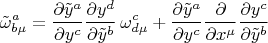
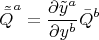

Относительно преобразований координат

пространства-времени
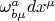
ведёт себя как 1-форма, а зарядовые векторы ведут себя как скаляры.
Давайте отдалимся от произвольных алгебр Ли, и спустимся к грешной земле - ну почти к Стандартной модели, но ограничимся только нуклонами (протоном и нейтороном) они образуют дублет по группе SU(2). Как вводится заряд? какой заряд будет для полей - бозонов SU(2)?
Написать связь между макроскопическими феноменологическими параметрами механической пробной частицы и параметрами определёнными в микроскопической квантовой теории поля?!! Не, это вопрос не ко мне. Может
grno поможет, потом
