Во-первых на С писать гораздо проще. Пусть результат и не столь же быстр.
Во-вторых, одним маленьким кусочком не обойтись если хотите получить ускорение вместо замедления. Всегда же есть накладные расходы на запуск внешней проги, в PARI это сотые доли секунды, значит внешняя прога должна полезно работать хотя бы десятые секунды. Тест накладных расходов в PARI:
Код:
{t0=getwalltime(); n=0; shag=10^2;
while((tt=getwalltime()-t0)<10000,\\Считаем сколько раз за примерно 10с сможем запустить внешнюю прогу
q=0; for(i=1,shag, q+=#externstr("cmd.exe /c cls")); n+=shag;
);
print("Speed: ",round(n/tt*1e3),"/c (",n," iterations)");
У меня выводит около 180 раз в секунду, значит накладные расходы примерно 5мс.
Перенести длинный if и цикл с setsearch/bittest в прогу будет недостаточно, они явно выполняются быстрее 10мс (у меня 17с на 10млн вместе с циклом по i, т.е. 1.7мкс). Разве что для тренировки. Но ускорения так не получить, скорее замедление в тысячи раз.
Переносить три isprime в прогу - трудно, числа большие, писать самому нормальный тест простоты откровенно влом, да и не факт что получится сильно быстрее isprime в PARI (помнится когда с Hugo занимались минимизацией цепочек, у меня простой тест простоты работал лишь немногим быстрее PARI и только для чисел меньше

).
В итоге в прогу стоит переносить сразу цикл по i с проверкой длинным if и bittest (это одна команда, а setsearch целая процедура) и возвратом списка кандидатов в том же 10млн отрезке i. Их будет 1.5млн из 10млн, это слишком много, фильтрация 7:1 вообще ни о чём. А выполняться внешняя прога будет точно дольше 1.5млн*54модуля*150тактов/3.5ГГц=3.5с (только три деления числа 192 битов на мелкое простое плюс 0.1с всё остальное), на самом деле время будет даже больше, раза в два. Экономия всего 13с (17с-4с) из 44с.
Выходит что isprime придётся таки делать в проге в каком-то виде, иначе про существенное ускорение говорить не приходится. Проверка делимости на простые

оставляет 35% исходных чисел, для трёх проверяемых чисел это даёт
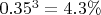
. Вот 23:1 уже неплохой коэффициент фильтрации, но 3*12250*3 делений (для трёх проверяемых чисел длиной по 192 бита) займут 1.5мс на каждый кандидат из 1/7 исходных. Пусть даже в 15 раз меньше, типа много составных не будут доходить до конца делений, всё равно это 0.1мс на кандидата и 150с на 1.5млн кандидатов после первой фильтрации 7:1. Замедление в несколько раз.
В итоге, если внешнюю прогу (не обязательно на асме, на любом языке) делать относительно простой, то заметного выигрыша скорости не получить.
Выход: во внешней проге делать всю основную работу (цикл по миллионам i, проверка по малым модулям, проверка псевдопростоты по средним модулям) и очень желательно работать не с длинными числами (а с короткими в арифметике по модулям) и не делениями. Но это уже не так просто. Помнится даже
специальную тему заводили про оптимизацию на асме, но до самой оптимизации там и не добрались.
YadryaraТак что Вы хотите перенести в асм (или С)?
Компилятор С кстати
есть уникально маленький, для простых программ достаточно. Но как к нему нормально подключить асм+AVX я пока не разобрался.