Там изюминка в том, чтобы допустить в части анализа, что
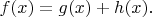
Тогда
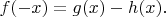
Затем надо сложить и вычесть.
Именно это очевидное действие здесь долго и нудно обсуждалось.
Могу предположить, откуда растет вопрос. В европейских школах часто учат: "Дети, никогда не начинайте доказательство с того, что нужно доказать - это страшная логическая ошибка!" Но в то же время иногда для построения основного доказательства нужно начать именно с того, что требуется доказать. У дочки в школе в таких случаях учат выделять такие предварительные рассуждения в отдельную часть и обязательно маркировать её "Jottings. Not part of the proof!":)
Сей (очень простой) факт упоминается в древней классической книжке Стейн, Вейс "Введение в гармонический анализ" в главе 4 о свойствах симметрии преобразования Фурье как тривиальный одномерный случай.