Гипотеза Римана доказана?

[SomePupil]

Предположительное доказательство [1]. Выложено в феврале этого года, пока цитирований нет. Вроде не фрик. Явных ляпов не нашел.

[1] Dettmers S. A Potential-Theoretic Approach to the Location of Zeros of the Riemann Zeta Function. – 2025.

[dsge]

Dettmers S. A Potential-Theoretic Approach to the Location of Zeros of the Riemann Zeta Function. – 2025.

Цитата:

While the logical structure appears sound and the conclusion rigorously derived based on the detailed analysis, the result’s significance necessitates careful and critical review by the mathematical community.

SomePupil в сообщении #1701787 писал(а):

Явных ляпов не нашел.

Полдела сделано. Осталось подождать оставшуюся часть математического коммьюнити.

[SomePupil]

dsge, да, автор сам сомневается

(Оффтоп)

Я на самом деле час писал пояснения, но при нажатии "отправить" произошла ошибка и весь текст пропал. Поэтому так. Получилось по образу и подобию этой темы)

[Anton_Peplov]

(Оффтоп)

SomePupil в сообщении #1701792 писал(а):

Я на самом деле час писал пояснения, но при нажатии "отправить" произошла ошибка и весь текст пропал.

Что, и кнопка "назад" в браузере не помогла? Если так, переходите на Chrome.

[icosahedron2]

Не могу проверить доказательство, так как знаком с гипотезой Римана только по книге Дербишира "Простая одержимость". Мне показались странными секции 5 и 6. Даже мне они кажутся тривиальными. Зачем уделять две секции тому, что можно уместить в 2-3 строки, сославшись на общеизвестные факты о дзета функции? ​

[dsge]

SomePupil в сообщении #1701787 писал(а):

Вроде не фрик.

https://www.researchgate.net/profile/Sebastian-Dettmers
https://www.linkedin.com/in/dettmers/

И у него хватает времени доказывать ГР.

[mihaild]

Theorem 4.1 писал(а):

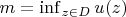
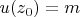
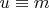
Theorem 4.1 (Strong Minimum Principle for Subharmonic Functions). Let $u$ be a subharmonic function on a domain (connected open set) $D \subset \mathbb{C}$. If $u$ is not identically constant, then $u$ cannot attain its infimum $m = \inf_{z \in D} u(z)$ at any interior point $z_0 \in D$. That is, if $u(z_0) = m$ for some $z_0 \in D$, then $u$ must be constant ($u \equiv m$). 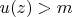Consequently, if $u$ is subharmonic and non-constant, $u(z) > m$ for all $z \in D$. 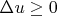This holds even if $u$ is only known to be subharmonic in the distributional sense ($\Delta u \ge 0$) and is upper semi-continuous. 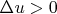If $u$ is strictly subharmonic ($\Delta u > 0$), it cannot be constant, thus it can never attain its infimum at an interior point (cf. Ransford, 1995, Corollary 3.3.6, p. 47; the principle is a cornerstone of potential theory).

Книгу, на которую автор ссылается, найти не удалось. И как-то непохоже на правду.
Возьмем $u(x, y) = x^2 + y^2$ в единичном круге, $\Delta u = 4$, но $u$ достигает минимума во внутренней точке $(0, 0)$.

[Sender]

И вики говорит, что для субгармонических функций известен принцип максимума, а вот минимум может достигаться во внутренних точках.
https://en.wikipedia.org/wiki/Subharmonic_function

[skobar]

mihaild в сообщении #1701800 писал(а):

Книгу, на которую автор ссылается, найти не удалось. И как-то непохоже на правду.
Возьмем $u(x, y) = x^2 + y^2$ в единичном круге, $\Delta u = 4$, но $u$ достигает минимума во внутренней точке $(0, 0)$.

Вот книжка, на которую ссылается автор:
https://drive.google.com/drive/folders/ ... sp=sharing
Естественно, такой ерунды как "Strong Minimum Principle for Subharmonic Functions" там нет. Более того, на странице 29 прямо говорится противоположное:
Note that in part (a), u can attain a local maximum or a global minimum without being constant on D.
Похоже, что автор спутал субгармонические и гармонические функции.

[sergey zhukov]

(Оффтоп)

SomePupil в сообщении #1701792 писал(а):

Я на самом деле час писал пояснения, но при нажатии "отправить" произошла ошибка и весь текст пропал. Поэтому так. Получилось по образу и подобию этой темы)

Я перед о правкой нажимаю Ctrl-A, Ctrl-C всегда.