Theorem 4.1 (Strong Minimum Principle for Subharmonic Functions). Let

be a subharmonic function on a domain (connected open set)

. If

is not identically constant, then

cannot attain its infimum
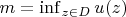
at any interior point

. That is, if
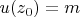
for some

, then

must be constant (
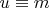
). Consequently, if

is subharmonic and non-constant,
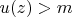
for all

. This holds even if

is only known to be subharmonic in the distributional sense (
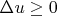
) and is upper semi-continuous. If

is strictly subharmonic (
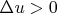
), it cannot be constant, thus it can never attain its infimum at an interior point (cf. Ransford, 1995, Corollary 3.3.6, p. 47; the principle is a cornerstone of potential theory).
Книгу, на которую автор ссылается, найти не удалось. И как-то непохоже на правду.
.