Anton_PeplovНа всякий случай (чтобы обо мне не думали слишком хорошо :), насчёт авторства того "изящного построения" - оно не моё. Подобное простейшее рассуждение есть в разных, встречавшихся мне текстах.
"Подвох" (если это называть подвохом) там действительно есть; и очень хорошо, что Вы это видите. Но это там всё-таки не подвох (в смысле обман читателя), а некоторое сознательно сделанное предположение. Понять, в чём оно заключается, лучше всего не в контексте с поначалу для читателя совершенно загадочными устройствами Алисы и Боба и их случайными нажатиями неких кнопок, а сразу в нормальном описании квантовомеханического эксперимента, пусть упрощённого и мысленного. (А манера рассказывать про такие опыты в форме загадки возникла в те давние годы, когда Белл и другие авторы, особенно Мермин (N.D. Mermin), пытались популяризировать эту тему для широкой публики, типа: "граждане, удивляйтесь, мир-то оказался квантовым, смотрите, какую
головоломку нам преподносит природа!" Эта традиция прижилась в статьях и книгах - она способствует привлечению внимания читателей.)
Раз Вы уже читаете учебник по КМ, то наверное наряду с "головоломным" описанием поймёте и обычное
квантовомеханическое. Спин электрона может показаться мало наглядным понятием для начинающего читателя, поэтому возьмём более наглядное понятие - "линейная поляризация фотона".
Устройство у Алисы (у Боба оно аналогичное) анализирует поляризацию фотона по признаку: горизонтальная (H) или вертикальная (V). Наглядно эти два состояния поляризации фотона,
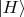
или
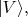
можно представить себе просто как два обычных вектора на плоскости - два декартовых орта

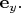
Для нас такая картина важна потому, что мы (с Вами) умеем повернуть орты в этой плоскости (на любой угол

против часовой стрелки) и написать разложения повёрнутых ортов
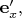
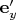
по исходным ортам

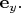
Так вот: символы повёрнутых состояний
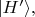
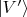
связаны с
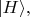

точно такими же равенствами. И с этими символами можно всё вычислять так же, как с обычными векторами. Например, скалярное произведение
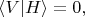
как и
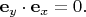
А знать всё это про повороты нужно потому, что направления поляризации жёстко заданы положением оптической системы внутри устройства. Далее для краткости буду называть устройство прибором. Фотон, влетающий в прибор Алисы, может не иметь определённой поляризации. Но он обязательно обнаружится одним из двух детекторов, расположенных на выходах двух каналов (H и V) оптической системы. Т.е. фотон обнаружится или в состоянии
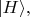
и тогда пусть в данном приборе на экране зажигается

или - в состоянии
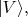
и тогда в приборе на экране зажигается

Если до того повернуть оптическую систему внутри прибора, то он будет работать аналогично, но только анализироваться будут повёрнутые направления поляризации:

зажигается, если фотон обнаруживается в состоянии
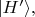
а

зажигается, если фотон обнаруживается в состоянии
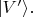
Об этом - т.е. повёрнута ли и на какой угол

анализирующая оптическая система, - говорят как о выборе измерительного базиса. Т.е.
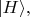

это один базис,
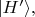
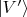
с каким-то конкретным значением

(таким, что новые направления ортов не совпадают со старыми) это другой базис, а ещё и с другим значением

- это уже ещё один базис, и так далее.
Кнопка "M" на приборе Алисы просто задаёт один из двух базисов - одно из двух положений оптической системы внутри прибора; обозначим его, скажем,
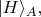
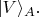
Кнопкой "N" оптическая система поворачивается в другое положение, так Алиса выбирает повёрнутый базис
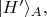
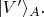
У Боба всё аналогично, но только базисы не обязательно такие же, как у Алисы; они могут быть повёрнутыми относительно Алисиных. Все эти базисы можно представлять себе как пары ортов в плоскости, перпендикулярной направлению прилёта фотонов в прибор.
Фотоны испускаются источником парами. Пусть поляризационное квантовое состояние

пар фотонов до прилёта в приборы описывается формулой, для простоты, аналогичной электронному спиновому синглету. Т.е.
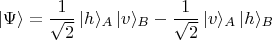
где
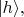
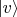
это тоже орты. В этой записи для краткости опущен знак "тензорного произведения"

между символами ортов. Согласно знаменитому принципу суперпозиции в КМ эта запись означает, например, что первый фотон может с амплитудой вероятности

обнаруживаться в приборе А в состоянии
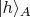 и при этом
и при этом второй фотон будет обнаруживаться в приборе В в состоянии
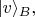 или
или наоборот - первый фотон может с амплитудой вероятности
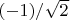
обнаруживаться в приборе А в состоянии
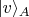 и при этом
и при этом второй фотон будет обнаруживаться в приборе В в состоянии
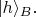
Вероятность равна квадрату модуля амплитуды вероятности. Который из двух фотонов первым обнаружится, не важно, а важно, что изначально у них нет определённой поляризации, но после обнаружения у одного фотона какой-то поляризации у второго будет ортогональное состояние поляризации.
Указанное состояние

обладает примечательным свойством - оно инвариантно к поворотам на один и тот же угол одновременно обоих ортов
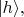
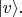
Т.е. оно равно такому же выражению

, в котором вместо
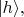
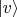
будут
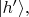
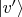
(это прямо проверяется с помощью формул поворота ортов). Поэтому мы можем полагать в выражении

что, например,
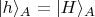
и
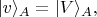
и это есть уже тот базис, который Алиса выбрала кнопкой "М" или "N", а
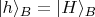
и
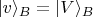
мы выразим через повёрнутые
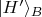
и
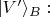
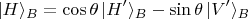
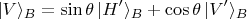
где

это угол, на который выбранный Бобом базис повёрнут относительно Алисиного базиса. Подставив это в

получаем
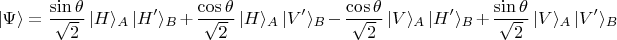
Согласно принципу суперпозиции здесь коэффициенты это амплитуды вероятностей событий, которые обозначены векторами состояний. Просматривая строчку с этим длинным равенством слева направо, видим, что:
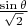
это амплитуда вероятности события
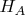
и
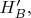
т.е. появления результатов
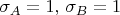
на экранах приборов Алисы и Боба;
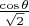
это амплитуда вероятности события
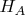
и
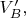
т.е. появления
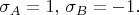
И так далее. Значения вероятностей
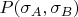
равны квадратам модулей амплитуд вероятностей. Таким образом:
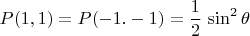
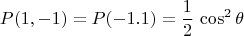
Следовательно, для среднего значения произведения
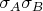
получаем:
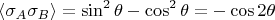
В литературе встречается описание выборов базиса, например, такое, как показано на рисунке ниже. Значки "M" и "N" указывают направление "горизонтальной поляризации" оптической системы в приборах Алисы и Боба относительно оси

в плоскости

Угол

это угол поворота базиса Боба относительно базиса Алисы; для четырёх разных выборов базисов значения этого угла равны
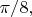
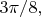
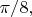
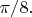
Величины
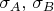
под знаками усреднения обозначены тоже буквами "M" и "N", соответственно выбору базиса:
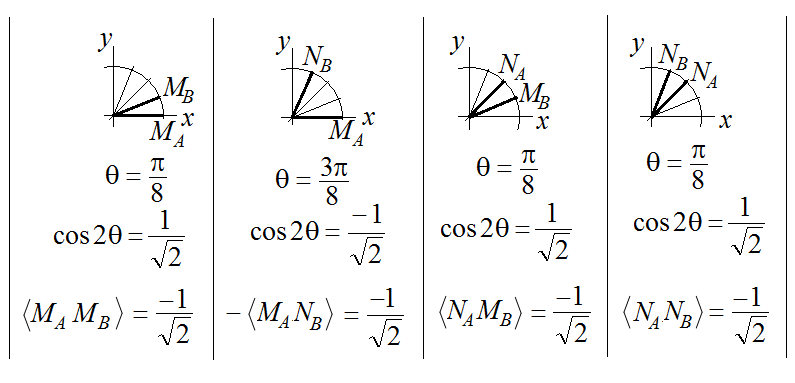
Таким образом, в этом примере КМ-формализм даёт
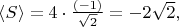
т.е.
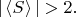
(И эксперименты этот результат или, по крайней мере, что-то в этом духе, уверенно подтверждают.)
Теперь о неравенстве Белла. Его вывод не имеет ничего общего с КМ-формализмом. Насколько понимаю, при выводе неравенств Белла предполагается, что у частиц вообще все величины всегда имеют некоторые значения. Предполагается, что все эти значения зависят от неких скрытых параметров

и воспринимаются нами как случайные величины. В этом принципиальное отличие от КМ: в КМ до акта измерения у фотона нет определённой поляризации, а в ТСП скрытые параметры содержат информацию, определяющую результаты всех возможных измерений над фотонами, даже если эти измерения никто не делает.
Т.е. в ТСП величины
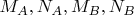
это именно случайные величины, они зависят от некоей совокупности скрытых параметров

, всегда имеют какие-то значения, для них есть какое-то неизвестное нам распределение вероятности, что-то типа
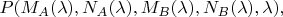
и по нему можно усреднить, как
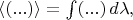
любое выражение с этими случайными переменными, в том числе и то выражение для
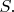
Величина

оказывается определённой вне зависимости от того, измеряются ли сразу все четыре случайные величины или не все.
"Головоломное" описание опыта составлено так, чтобы оно выглядело похожим на квантовомеханическую постановку эксперимента. Алиса нажимает, допустим, кнопку "М" и экран показывает значение

только этой случайной переменной. Но в ТСП при этом существует и значение
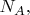
просто оно не выведено на экран гипотетического ТСП-прибора, который мог бы показывать сразу все величины (и хорошо бы ещё и скрытые параметры бы показывал :).
То, что Алиса и Боб должны нажимать кнопки в случайном порядке, - не играет роли для вычисления

ни в ТСП, ни в КМ. В любом случае мы в итоге интересуемся статистикой результатов отдельно для разных комбинаций. Поэтому можно считать, что сначала измеряются только

и
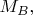
и по этим данным в итоге вычисляется среднее арифметическое
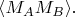
Затем - только

и
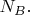
И так далее, все четыре комбинации - поочерёдно. Примерно об этом я и написал в предыдущих сообщениях. В том числе сказал, что тот вывод неравенства Белла предложен там лишь для начала, как простейший, а дальше надо вникать в "дьявола в деталях" в расчётах вероятностей, и упомянул, что для вывода неравенств Белла нужна ТСП.
Если Вы согласны с этим, то я продолжу "шпарить по книжке", потому что вопросы, которые мне действительно непонятны, еще впереди.
Согласен в том, что да, надо дальше внимательно разбираться с более серьёзным выводом неравенств Белла, если продолжать интересоваться их обсуждением.
Конечно, читайте книгу. Без сомнения. И вопросы задавайте. Не могу сказать, что я большой спец в таких сюжетах (и ТСП с сопутствующей ей философией я недолюбливаю); наверное, не на всё смогу ответить. Но есть ведь и другие участники форума; может быть, и они подключатся.
(
P.S. 11.09.2025. Исправил ошибку в строчке с длинным равенством: в двух последних слагаемых синус и косинус поменялись местами.)