Написал, как мне (Bell.2)-(Bell.4) видятся "на пальцах". Поскольку я не знаток теорвера на математическом уровне строгости, то для меня "на пальцах" означает: не пользоваться теоремами теорвера, а оценивать вероятность события, как дробь - отношение, сколько раз случилось интересующее событие, к очень большому числу всех случившихся событий (обычно так и оценивают вероятности из экспериментов). Сначала, себе для ясности, разбираю элементарную картину без скрытых параметров (СП), а затем чуть более сложную с СП:
Пусть есть мешок с частицами. На каждой частице написано одно число:
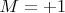
или
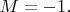
Источник посылает из мешка частицы парами: одну частицу Алисе, другую Бобу. Всего в ходе опыта посылается

пар:
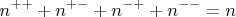
Здесь обозначено:
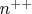
- столько раз Алиса получила
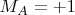
и Боб получил
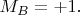
Остальные обозначения аналогичны этому. Разделив обе стороны этого равенства на

увидим дроби, четыре штуки (их сумма равна единице). Это оценки для вероятностей
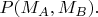
Буду такие дроби для краткости называть вероятностями. Через них оценивается коррелятор
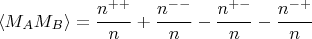
Суммарные вероятности получаются делением на

равенств


Через них оцениваются средние значения показаний приборов Алисы и Боба:
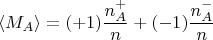
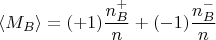 Пример без корреляции:
Пример без корреляции:Если источник раздаёт частицы совершенно случайным образом, то для оценки можно считать, что среди числа
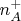
случаев с
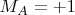
долю
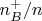
составляют случаи с
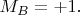
Поэтому
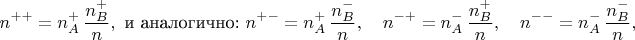
Разделив на

получаем равенства с произведениями вероятностей независимых событий:
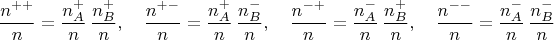
Подставив это в выражение для коррелятора, видим, что
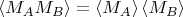
Такая факторизация коррелятора служит признаком того, что

и

- независимые случайные величины.
Пример c корреляцией:Пусть источник раздаёт Алисе и Бобу частицы всегда с противоположным знаком. Плюс или минус - пусть будут равновероятными. Тогда:
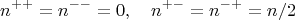
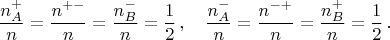

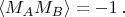
Пусть

есть в общем случае многокомпонентный "вектор", с дискретными значениями компонент. Источник посылает Алисе и Бобу частицы со значением (многокомпонентным)

Обоим - одинаковое

но от раза к разу оно может случайным образом меняться. Пусть показания
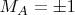
и
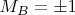
приборов у Алисы и Боба являются некоторыми функциями от

Функция
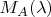
пусть зависит только от части компонент "вектора"

обозначу эту часть как
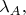
а функция
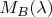
пусть зависит от остальной части,
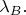
Но ниже я такую разбивку

на части явно не выписываю, для краткости.
Однозначных обратных функций здесь нет. Невозможно по значению
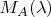
вычислить полностью

и таким путём узнать
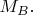
Т.е. зная

можно предсказать
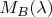
и
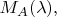
а зная только значение
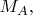
нельзя предсказать значение
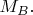
Также и наоборот: по

нельзя узнать
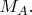
Значит, можем полагать, что

и

- независимые величины. Они случайные из-за случайности

Индексом

отметим числа, относящиеся к случаям с данным конкретным

В ходе опыта параметр принимал данное значение

какое-то очень большое число раз
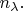
При этом у Алисы
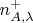
раз прибор показал
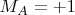
и
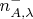
раз показал
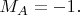
Аналогично и у Боба. Так что:
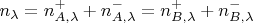
Разделив это на
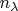
увидим здесь дроби, являющиеся оценками для нормированных вероятностей
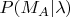
и
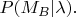
Рассмотрим число
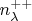
- столько раз при заданном

было одновременно
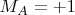
и
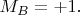
Поскольку

и

независимы, это число раз можно оценить как долю
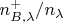
от числа
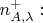
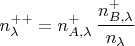
Правую сторону этого равенства умножим и тут же разделим на
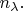
Затем просуммируем такие равенства по

И разделим обе стороны на полное число событий, т.е. на
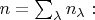
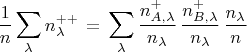
Понимая здесь дроби как оценки вероятностей, заключаю, что получилось равенство
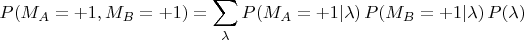
Аналогично получается и для остальных комбинаций плюсов и минусов, т.е. пришли к равенству типа (Bell.4):
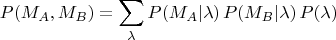 Пример ТСП-модели с корреляцией. "Фотоны" со скрытыми параметрами:
Пример ТСП-модели с корреляцией. "Фотоны" со скрытыми параметрами:Пусть источник посылает "фотоны" двух равновероятных сортов: с определённым вектором

или с ортогональным ему вектором

Чертежи на предыдущем моём
рисунке пронумеруем буквами слева направо как а), б), в), г); на формулы там теперь не смотрим вовсе.
Представим себе там вектор

как орт оси

чуть-чуть повёрнутый против часовой стрелки на очень малый угол. И, аналогично,

это орт оси

чуть-чуть повёрнутый на такой же малый угол против часовой стрелки. (Такой маленький поворотик позволит далее в модели приборов избежать хлопот с направлением
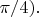
Корреляция пусть заключается в том, что если Алисе послан "фотон"

то Бобу - "фотон"

И наоборот: когда Алисе послан

Бобу посылается
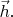
Эти "векторы поляризации фотонов" играют роль скрытых параметров, управляющих работой приборов.
Модель приборов пусть будет вот какая. На упомянутых рисунках жирная линия изображает "ось" прибора. Пусть прибор доворачивает вектор поляризации фотона: либо укладывает его вдоль своей оси, и тогда показывает на экране

либо ставит его перпендикулярно своей оси, и тогда показывает

По правилу: если на рисунке угол между осью прибора и вектором фотона меньше или равен

то экран покажет

а иначе экран покажет

Подчеркну принципиальное отличие этой ТСП-модели от КМ. В КМ вектор состояния линейной поляризации фотона, например,

в общем случае не позволяет предсказать показание экрана, предсказывается только вероятность: с вероятностью

будет показание

либо с вероятностью

будет показание

где

это угол между вектором состояния поляризации фотона и осью прибора. А в данной ТСП-модели "вектор поляризации фотона" даёт не вероятности, а инструкцию прибору: какое показание прибор должен выдать на экран.
Для случая а) находим, глядя на чертёж:
При
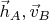
(т.е. если к Алисе пришёл фотон

а к Бобу -
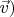
будет
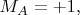
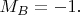
При
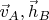
будет
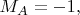
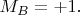
Поскольку это равновероятные события, то
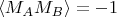
Для случая б):
При
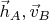
будет
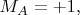
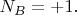
При
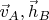
будет
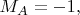
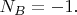
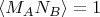
Для случая в):
При
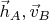
будет
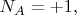
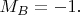
При
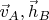
будет
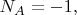
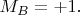
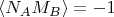
Для случая г):
При
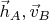
будет
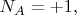
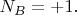
При
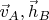
будет
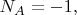
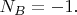
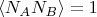
В каждом из этих случаев усреднённые показания каждого прибора равны нулю. Корреляторы отличны от нуля. При этом, как видим,
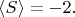
Неравенство Белла
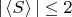
не нарушено.
Эту же модель можно изложить и в духе (Bell.4), но выглядит это тривиально. В любом из случаев a) - г) сумма по

содержит всего два слагаемых - одно для варианта
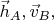
(условно обозначим его как
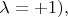
другое - для
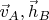
(условно:
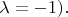
Для обоих слагаемых
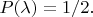
Пусть речь идёт, например, о случае а). Под знаком суммы по

наряду с сомножителем
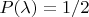
отличны от нуля только
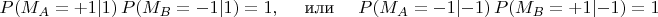
Т.е. из всех
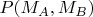
отличны от нуля только

Поэтому и получается
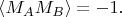
Аналогично рассматриваются случаи б) - г).
Можно и другие модели ТСП-приборов придумывать при том же источнике "фотонов", неравенство Белла при этом не нарушается. Например, пусть прибор показывает

если угол между "вектором фотона" меньше
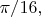
а иначе - показывает

Тогда в случаях а) - г) получается
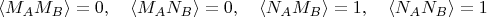
Как видим,
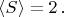
Неравенство
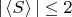
не нарушено.